题目内容
已知幂函数f(x)=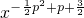 (p∈Z)在(0,+∞)上是增函数,且在其定义域内是偶函数.
(p∈Z)在(0,+∞)上是增函数,且在其定义域内是偶函数.
(1)求p的值,并写出相应的函数f(x).
(2)对于(1)中的f(x),是否存在正实数m,使得g(x)=-f(x)+(2m-1)x+1在区间[-1,1]上的值域是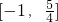 ,若存在,求出m的值;若不存在,说明理由.
,若存在,求出m的值;若不存在,说明理由.
解:(1)因为幂函数f(x)=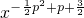 在(0,+∞)上是增函数,
在(0,+∞)上是增函数,
所以- p2+p+
p2+p+ >0,解得-1<p<3.
>0,解得-1<p<3.
∵P是整数,∴P的值为0,1,2,
又幂函数在其定义域内是偶函数,所以p=1.
∴函数f(x)=x2.
(2)存在正实数m,使得g(x)=-f(x)+(2m-1)x+1在区间[-1,1]上的值域是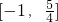 .
.
∵f(x)=x2,
∴g(x)=-f(x)+(2m-1)x+1=-x2+(2m-1)x+1,
∴g(-1)=-1-2m+1+1=1-2m,
g(1)=-1+2m-1=2m-1,
∵g(x)在区间[-1,1]上的值域是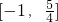 ,
,
∴1-2m=-1,或2m-1=-1.
当1-2m=-1时,m=1,g(x)=-x2+x+1=-(x- )2+
)2+
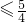 ,
,
∴m=1时,g(x)在区间[-1,1]上的值域是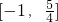 ,成立;
,成立;
当2m-1=-1时,m=0,g(x)=-x2-x+1=-(x+ )2+
)2+
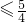 ,
,
∴m=0时,g(x)在区间[-1,1]上的值域是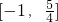 ,成立;
,成立;
综上所述,存在是存在正实数m=1,
使得g(x)=-f(x)+(2m-1)x+1在区间[-1,1]上的值域是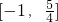 .
.
分析:(1)因为幂函数f(x)=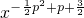 在(0,+∞)上是增函数,所以-
在(0,+∞)上是增函数,所以- p2+p+
p2+p+ >0,解得-1<p<3由幂函数在其定义域内是偶函数且p∈Z,所以p=1,由此能求出函数f(x).
>0,解得-1<p<3由幂函数在其定义域内是偶函数且p∈Z,所以p=1,由此能求出函数f(x).
(2)由f(x)=x2,知g(x)=-f(x)+(2m-1)x+1=-x2+(2m-1)x+1,故g(-1)=-1-2m+1+1=1-2m,g(1)=-1+2m-1=2m-1,由g(x)在区间[-1,1]上的值域是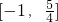 ,知1-2m=-1,或2m-1=-1.由此能求出正实数m.
,知1-2m=-1,或2m-1=-1.由此能求出正实数m.
点评:本题考查幂函数的概念和性质,是基础题.解题时要认真审题,仔细解答,注意二次函数的性质的灵活运用.
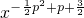 在(0,+∞)上是增函数,
在(0,+∞)上是增函数,所以-
 p2+p+
p2+p+ >0,解得-1<p<3.
>0,解得-1<p<3.∵P是整数,∴P的值为0,1,2,
又幂函数在其定义域内是偶函数,所以p=1.
∴函数f(x)=x2.
(2)存在正实数m,使得g(x)=-f(x)+(2m-1)x+1在区间[-1,1]上的值域是
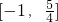 .
.∵f(x)=x2,
∴g(x)=-f(x)+(2m-1)x+1=-x2+(2m-1)x+1,
∴g(-1)=-1-2m+1+1=1-2m,
g(1)=-1+2m-1=2m-1,
∵g(x)在区间[-1,1]上的值域是
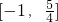 ,
,∴1-2m=-1,或2m-1=-1.
当1-2m=-1时,m=1,g(x)=-x2+x+1=-(x-
 )2+
)2+
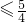 ,
,∴m=1时,g(x)在区间[-1,1]上的值域是
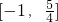 ,成立;
,成立;当2m-1=-1时,m=0,g(x)=-x2-x+1=-(x+
 )2+
)2+
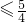 ,
,∴m=0时,g(x)在区间[-1,1]上的值域是
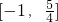 ,成立;
,成立;综上所述,存在是存在正实数m=1,
使得g(x)=-f(x)+(2m-1)x+1在区间[-1,1]上的值域是
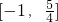 .
.分析:(1)因为幂函数f(x)=
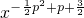 在(0,+∞)上是增函数,所以-
在(0,+∞)上是增函数,所以- p2+p+
p2+p+ >0,解得-1<p<3由幂函数在其定义域内是偶函数且p∈Z,所以p=1,由此能求出函数f(x).
>0,解得-1<p<3由幂函数在其定义域内是偶函数且p∈Z,所以p=1,由此能求出函数f(x).(2)由f(x)=x2,知g(x)=-f(x)+(2m-1)x+1=-x2+(2m-1)x+1,故g(-1)=-1-2m+1+1=1-2m,g(1)=-1+2m-1=2m-1,由g(x)在区间[-1,1]上的值域是
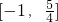 ,知1-2m=-1,或2m-1=-1.由此能求出正实数m.
,知1-2m=-1,或2m-1=-1.由此能求出正实数m.点评:本题考查幂函数的概念和性质,是基础题.解题时要认真审题,仔细解答,注意二次函数的性质的灵活运用.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目