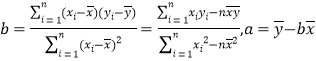题目内容
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 在
在![]() 上的单调区间;
上的单调区间;
(3)求![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(1)a=2,b=-4;(2)![]() 的增区间为
的增区间为 ![]() ;减区间为
;减区间为![]() ;(3)13.
;(3)13.
【解析】
(1)先对f(x)求导,把x=1代入导数式即可解出曲线在![]() 处的斜率k;把x=1代入原函数即可解出切点纵坐标,建立一个关于a和b的二元一次方程组,解方程可得a,b的值;
处的斜率k;把x=1代入原函数即可解出切点纵坐标,建立一个关于a和b的二元一次方程组,解方程可得a,b的值;
(2)求出f(x)的导数,由导数大于0,可得增区间;导数小于0,可得减区间;
(3)分别求出f(x)在区间[﹣3,1]上的极值和区间端点处的函数值,比较大小找出最大的值,即为函数在该闭区间上的最大值。
(1) 函数 ![]() 的导数为
的导数为 ![]() ,
,
曲线 ![]() 在点
在点 ![]() 处的切线斜率为
处的切线斜率为![]() ,
,
切点为![]() ,
,
由切线方程为 ![]() ,可得
,可得 ![]() ,
,![]() ,
,
解得![]() .
.
(2) 函数 ![]() 的导数
的导数![]() ,由
,由 ![]() ,可得
,可得 ![]() 或
或 ![]() ;由
;由 ![]() ,可得
,可得 ![]() .则 f(x) 的增区间为
.则 f(x) 的增区间为 ![]() ,
,![]() ;减区间为
;减区间为 ![]() .
.
(3) 由(2)可得 f(x) 的两极值点-2,![]() ,
,
![]() ,
,![]() ,
,
又 ![]() ,
,![]() .
.
故 y=f(x) 在 ![]() 上的最大值为 13.
上的最大值为 13.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据.
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)试根据(1)求出的线性回归方程,预测燃放烟花爆竹的天数为9的雾霾天数.
相关公式: