题目内容
设函数y=f（x）在（a，b）上的导函数为f′（x），f′（x）在（a，b）上的导函数为f″（x），若在a，b）上，f″（x）＜0恒成立，则称函数函数f（x）在（a，b）上为“凸函数”．已知当m≤2时，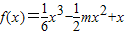
在（-1，2）上是“凸函数”．则f（x）在（-1，2）上（ ）A．既有极大值，也有极小值
B．既有极大值，也有最小值
C．有极大值，没有极小值
D．没有极大值，也没有极小值
【答案】分析：根据函数恒成立，得出m的值，利用函数单调性 得出结果．
解答：解：因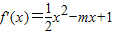
，f″（x）=x-m＜0对于x∈（-1，2）恒成立．
∴m＞（x）max=2，又当m=2时也成立，有m≥2．而m≤2，∴m=2．
于是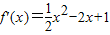
，由f′（x）=0x=
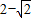或x=2+
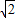（舍去），
f（x）（-1，2-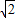
）上递增，在（2-
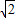，2）上递减，
只有C正确．
故选C
点评：本题主要考查导数和函数知识及利用导数判断函数单调性，属于基础知识，基本运算的考查．
解答：解：因
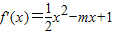，f″（x）=x-m＜0对于x∈（-1，2）恒成立．∴m＞（x）max=2，又当m=2时也成立，有m≥2．而m≤2，∴m=2．
于是
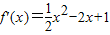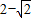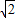，由f′（x）=0x=或x=2+（舍去），f（x）（-1，2-
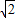）上递增，在（2-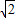，2）上递减，只有C正确．
故选C
点评：本题主要考查导数和函数知识及利用导数判断函数单调性，属于基础知识，基本运算的考查．
练习册系列答案
相关题目
设函数y=f（x）在（-∞，+∞）内有定义．对于给定的正数K，定义函数 fk(x)=
，取函数f（x）=2-x-e-x．若对任意的x∈（+∞，-∞），恒有fk（x）=f（x），则（ ）
|
| A、K的最大值为2 |
| B、K的最小值为2 |
| C、K的最大值为1 |
| D、K的最小值为1 |