题目内容
已知命题p:方程x2+mx+4=0有两个不等的负实数根.命题q:方程4x2+4(m-1)x+1=0无实数根.若“p或q”为真命题,“p且q”为假命题,求m的取值范围.
答案:
解析:
解析:
|
解析:先将p、q中m的范围求出,然后根据“p或q”为真,“p且q”为假,可知p和q中必是一真一假,则分两种情况列出不等式组求解,由p得 由q知, 则0<m<2 ∵“p或q”为真,“p且q”为假 ∴p为真,q为假,或p为假q为真 则 |

练习册系列答案
相关题目
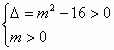 则m>4
则m>4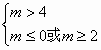 或
或