题目内容
已知p:x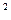 -8x-20>0,q:x
-8x-20>0,q:x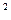 -2x+1-a
-2x+1-a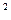 >0。若p是q的充分不必要条件,求正实数a的取值范围。
>0。若p是q的充分不必要条件,求正实数a的取值范围。
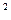 -8x-20>0,q:x
-8x-20>0,q:x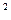 -2x+1-a
-2x+1-a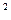 >0。若p是q的充分不必要条件,求正实数a的取值范围。
>0。若p是q的充分不必要条件,求正实数a的取值范围。正实数a的取值范围是0<a≤3
解不等式x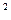 -8x-20>0得p:A={x|x>10,或x<-2}。
-8x-20>0得p:A={x|x>10,或x<-2}。
解不等式x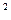 -2x+1-a
-2x+1-a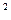 >0得q:B={x|x>1+a,或x<1-a,a>0}。
>0得q:B={x|x>1+a,或x<1-a,a>0}。
依题意,p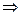 q但q ≠> p,说明A
q但q ≠> p,说明A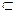 B。
B。
于是有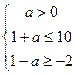 ,解得0<a≤3。
,解得0<a≤3。
∴正实数a的取值范围是0<a≤3。
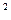 -8x-20>0得p:A={x|x>10,或x<-2}。
-8x-20>0得p:A={x|x>10,或x<-2}。解不等式x
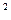 -2x+1-a
-2x+1-a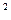 >0得q:B={x|x>1+a,或x<1-a,a>0}。
>0得q:B={x|x>1+a,或x<1-a,a>0}。依题意,p
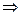 q但q ≠> p,说明A
q但q ≠> p,说明A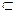 B。
B。于是有
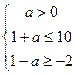 ,解得0<a≤3。
,解得0<a≤3。∴正实数a的取值范围是0<a≤3。

练习册系列答案
相关题目
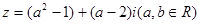 ,则“
,则“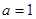 ”是“
”是“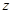 为纯虚数”的
为纯虚数”的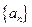 的前
的前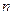 项的和
项的和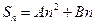 是数列
是数列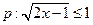 ,
,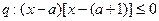 ,若
,若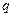 是
是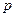 的必要而不充分条件,则实数
的必要而不充分条件,则实数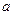 的取值范围是( )
的取值范围是( )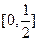
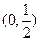
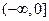 ∪
∪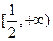
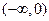 ∪
∪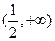
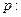
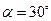 是
是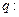
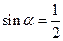 成立的 ( )
成立的 ( ) 说法正确的是_____
说法正确的是_____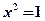 则
则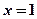 ”否命题为:
”否命题为: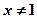 ;
;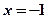 ”是
”是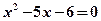 的必要不充分条件;
的必要不充分条件;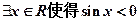 ”的否定是:
”的否定是: ,均有“
,均有“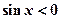 ”;
”;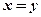 ,则
,则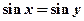 ”的逆否命题为真。
”的逆否命题为真。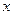 的一元二次不等式
的一元二次不等式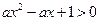 对于一切实数
对于一切实数