题目内容
已知ab≠0,求证:a+b=1的充要条件是a3+b3+ab-a2-b2=0.
证明略
证明(必要性)
∵a+b=1,∴a+b-1=0, 2分
∴a3+b3+ab-a2-b2=(a+b)(a2-ab+b2)-(a2-ab+b2) 5分
=(a+b-1)(a2-ab+b2)="0. " 7分
(充分性)
∵a3+b3+ab-a2-b2=0,
即(a+b-1)(a2-ab+b2)=0, 9分
又ab≠0,∴a≠0且b≠0,
∴a2-ab+b2=(a- b2>0,
b2>0,
∴a+b-1=0,即a+b="1, " 12分
综上可知,当ab≠0时,a+b=1的充要条件是
a3+b3+ab-a2-b2="0. " 14分
∵a+b=1,∴a+b-1=0, 2分
∴a3+b3+ab-a2-b2=(a+b)(a2-ab+b2)-(a2-ab+b2) 5分
=(a+b-1)(a2-ab+b2)="0. " 7分
(充分性)
∵a3+b3+ab-a2-b2=0,
即(a+b-1)(a2-ab+b2)=0, 9分
又ab≠0,∴a≠0且b≠0,
∴a2-ab+b2=(a-
 b2>0,
b2>0,∴a+b-1=0,即a+b="1, " 12分
综上可知,当ab≠0时,a+b=1的充要条件是
a3+b3+ab-a2-b2="0. " 14分

练习册系列答案
相关题目
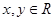 ,则“
,则“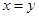 ”是“
”是“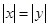 ”的
”的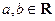 ,命题
,命题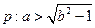 ;命题
;命题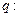 直线
直线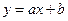 与圆
与圆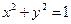 相交,则
相交,则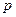 是
是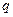 的
的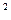 -8x-20>0,q:x
-8x-20>0,q:x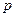 :
: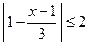 ,
,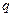 :
: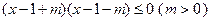
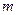 的取值范围。
的取值范围。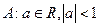 ,
, 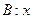 的二次方程
的二次方程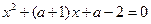 的一个根大于零,
的一个根大于零,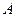 是
是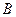 的( )
的( )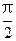 ,则“x sin2x<1”是“x sinx<1”的
,则“x sin2x<1”是“x sinx<1”的