题目内容
设a为实数,函数f(x)=2x2+(x-a)|x-a|.
(1)若f(0)≥1,求a的取值范围;
(2)求f(x)的最小值;
(3)设函数h(x)=f(x),x∈(a,+∞),求不等式h(x)≥1的解集.
(1)若f(0)≥1,求a的取值范围;
(2)求f(x)的最小值;
(3)设函数h(x)=f(x),x∈(a,+∞),求不等式h(x)≥1的解集.
(1)若f(0)≥1,则-a|a|≥1⇒
⇒a≤-1
(2)当x≥a时,f(x)=3x2-2ax+a2,∴f(x)min=
=
,
如图所示:
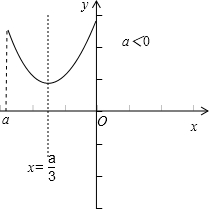
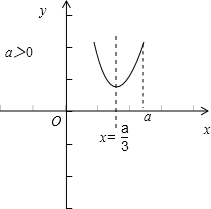
当x≤a时,f(x)=x2+2ax-a2,
∴f(x)min=
=
.
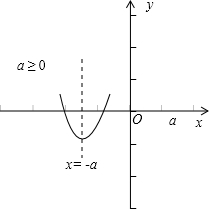
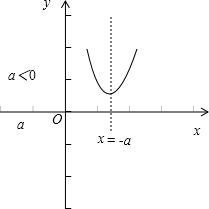
综上所述:f(x)min=
.
(3)x∈(a,+∞)时,h(x)≥1,
得3x2-2ax+a2-1≥0,△=4a2-12(a2-1)=12-8a2
当a≤-
或a≥
时,△≤0,x∈(a,+∞);
当-
<a<
时,△>0,得:
即
综上可得,
当a∈(-∞,-
)∪(
,+∞)时,不等式组的解集为(a,+∞);
当a∈(-
,-
)时,不等式组的解集为(a,
]∪[
,+∞);
当a∈[-
,
]时,不等式组的解集为[
,+∞).
|
(2)当x≥a时,f(x)=3x2-2ax+a2,∴f(x)min=
|
|
如图所示:


当x≤a时,f(x)=x2+2ax-a2,
∴f(x)min=
|
|


综上所述:f(x)min=
|
(3)x∈(a,+∞)时,h(x)≥1,
得3x2-2ax+a2-1≥0,△=4a2-12(a2-1)=12-8a2
当a≤-
| ||
| 2 |
| ||
| 2 |
当-
| ||
| 2 |
| ||
| 2 |
|
即
|
综上可得,
当a∈(-∞,-
| ||
| 2 |
| ||
| 2 |
当a∈(-
| ||
| 2 |
| ||
| 2 |
a-
| ||
| 3 |
a+
| ||
| 3 |
当a∈[-
| ||
| 2 |
| ||
| 2 |
a+
| ||
| 3 |

练习册系列答案
相关题目
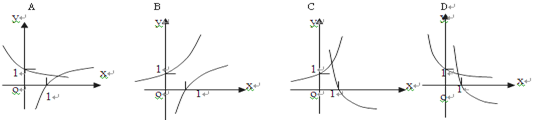
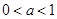 时,在同一坐标系中,函数
时,在同一坐标系中,函数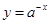 与
与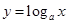 的图像是( )
的图像是( )