Question

已知常数a、b、c都是实数,函数f(x)=+x²+bx+c的导函数为f′(x).

(1)设a=f′(2),b=f′(1),c=f′(0),求函数f(x)的解析式;

(2)如果方程f′(x)=0的两个实数根分别为γ、β,并且1＜γ＜β＜2.问:是否存在正整数n₀,使得|f′(n₀)|≤?请说明理由.

Answer 1

解:(1)f′(x)=x²+ax+b,

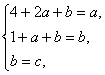∴解得

∴f(x)=x²-3x-3.

(2)∵f′(x)=0的两根为γ、β,∴f′(x)=(x-γ)(x-β).∵1＜γ＜β＜2,∴f′(1)=(1-γ)(1-β)＞0,f′(2)=(2-γ)(2-β)＞0.

∴f′(1)·f′(2)=(1-γ)(1-β)(2-γ)(2-β)=［(γ-1)(2-γ)］·［(β-1)(2-β)］

≤()²·()²=.

∴0＜f′(1)·f′(2)≤.∵f′(1)＞0,f′(2)＞0,∴0＜f′(1)≤或0＜f′(2)≤.

∴存在n₀=1或n₀=2使|f′(n₀)|≤成立.