题目内容
已知常数a、b、c都是实数，函数
的导函数为f ′（x）
（Ⅰ）设a=f ′（2），b=f ′（1），c=f ′（0），求函数f（x）的解析式；
（Ⅱ）设 f′（x）=（x﹣γ）（x﹣β），且1＜γ≤β＜2，求f ′（1）
f ′（2）的取值范围．
的导函数为f ′（x）（Ⅰ）设a=f ′（2），b=f ′（1），c=f ′（0），求函数f（x）的解析式；
（Ⅱ）设 f′（x）=（x﹣γ）（x﹣β），且1＜γ≤β＜2，求f ′（1）
f ′（2）的取值范围． （Ⅰ）解：由题意可得，f ′（x）=x2+ax+b．
∴
，
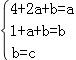解得：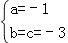
．
∴
．
（II）∵f ′（x）=（x﹣γ）（x﹣β）．
又 1＜γ≤β＜2，
∴f ′（1）=（1﹣γ）（1﹣β）＞0，f ′（2）=（2﹣γ）（2﹣β）＞0
∴f ′（1）
f ′（2）=（1﹣γ）（1﹣β）（2﹣γ）（2﹣β）
=[（γ﹣1）（2﹣γ）]
[（β﹣1）（2﹣β）]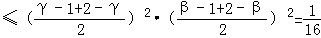 
∴
∴
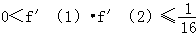
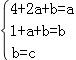，解得：
． ∴
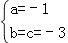．（II）∵f ′（x）=（x﹣γ）（x﹣β）．
又 1＜γ≤β＜2，
∴f ′（1）=（1﹣γ）（1﹣β）＞0，f ′（2）=（2﹣γ）（2﹣β）＞0
∴f ′（1）
f ′（2）=（1﹣γ）（1﹣β）（2﹣γ）（2﹣β） =[（γ﹣1）（2﹣γ）]
[（β﹣1）（2﹣β）] ∴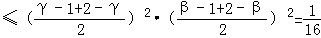
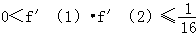
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
的导函数为f′（x）
+
x2+bx+c的导函数为f′(x).
?请说明理由.