题目内容
(本小题满分12分)已知△ABC的面积S满足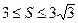 ,且
,且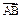 ·
·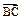 =6,
=6,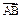 与
与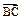 的夹角为
的夹角为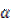 。(1)求
。(1)求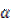 的取值范围;
的取值范围;
(2)若函数f(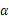 )=sin2
)=sin2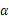 +2sin
+2sin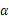 cos
cos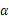 +3cos2
+3cos2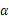 ,求f(
,求f(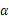 )的最小值,并指出取得最小值时的
)的最小值,并指出取得最小值时的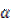 。
。
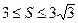 ,且
,且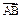 ·
·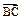 =6,
=6,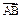 与
与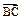 的夹角为
的夹角为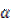 。(1)求
。(1)求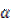 的取值范围;
的取值范围;(2)若函数f(
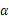 )=sin2
)=sin2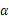 +2sin
+2sin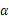 cos
cos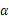 +3cos2
+3cos2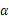 ,求f(
,求f(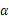 )的最小值,并指出取得最小值时的
)的最小值,并指出取得最小值时的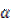 。
。(1)θ∈〔0,π〕∴θ∈〔,〕
(2)f(θ) min= =
(2)f(θ) min= =
(1)由题意知
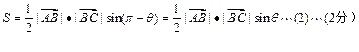
由②÷①得=tanθ即3tanθ=S……(3分)?
由3≤S≤3得3≤3tanθ≤3……(4分)?
又θ为 与
与 的夹角,∴θ∈〔0,π〕∴θ∈〔,〕……(6分)
的夹角,∴θ∈〔0,π〕∴θ∈〔,〕……(6分)
(2)f(θ)=sin2θ+2sinθcosθ+3cos2θ=1+sin2θ+2cos2θ?
∴f(θ)=2+sin2θ+cos2θ=2+sin(2θ+)……(9分)?
∵θ∈〔,〕,∴2θ+∈〔, 〕?
∴2θ+=,即θ=时,f(θ) min= =……(12分)

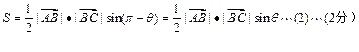
由②÷①得=tanθ即3tanθ=S……(3分)?
由3≤S≤3得3≤3tanθ≤3……(4分)?
又θ为
 与
与 的夹角,∴θ∈〔0,π〕∴θ∈〔,〕……(6分)
的夹角,∴θ∈〔0,π〕∴θ∈〔,〕……(6分)(2)f(θ)=sin2θ+2sinθcosθ+3cos2θ=1+sin2θ+2cos2θ?
∴f(θ)=2+sin2θ+cos2θ=2+sin(2θ+)……(9分)?
∵θ∈〔,〕,∴2θ+∈〔, 〕?
∴2θ+=,即θ=时,f(θ) min= =……(12分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
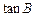 =
=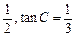 ,且最长边为
,且最长边为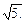
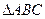 中,角
中,角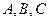 所对的边分别为
所对的边分别为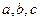 ,且满足
,且满足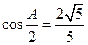 ,
,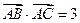 . (I)求
. (I)求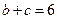 ,求
,求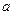 的值.
的值. 分别是角A,B,C的对边,
分别是角A,B,C的对边, ,且
,且 ∥
∥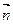
 若
若 ,求
,求 的最大值。
的最大值。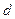 ;②A点处对M、N两点的俯角分别为
;②A点处对M、N两点的俯角分别为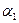 和
和 ;B点处对M、N两点的俯角分别为
;B点处对M、N两点的俯角分别为 和
和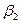 ;请同学们在示意图中标出这四个俯角并用文字和公式写出计算M,N间的距离的步骤.
;请同学们在示意图中标出这四个俯角并用文字和公式写出计算M,N间的距离的步骤.
 (2)在△ABC 中,若AB=2,AC=2BC,求△ABC面积的最大值.
(2)在△ABC 中,若AB=2,AC=2BC,求△ABC面积的最大值.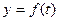 是某港口水的深度
是某港口水的深度 (米)关于时间
(米)关于时间 (时)的函数,其中
(时)的函数,其中 ,下表是该港口某一天从0时至24时记录的时间
,下表是该港口某一天从0时至24时记录的时间 的图象,下面的函数中最能近似地表示表中数据对应关系的函数是( )
的图象,下面的函数中最能近似地表示表中数据对应关系的函数是( ) ,
,
 ,
, ,
, ,
,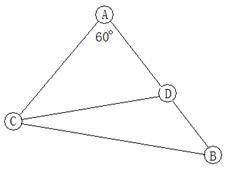
 海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘轮船之间的距离为 海里.
海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘轮船之间的距离为 海里. 
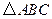 中,
中,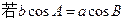 ,则此三角形为( )
,则此三角形为( )