题目内容
将一颗质地均匀的骰子（它是一种各面上分别标有点数1、2、3、4、5、6的正方体玩具）先后抛掷2次，记第一次出现的点数为m，记第二次出现的点数为n，向量
，
，则
和
共线的概率为（ ）A．
B．
C．
D．
【答案】分析：根据题意，用（m，n）表示连续抛掷两枚骰子得到的点数，列表可得（m，n）的情况数目，由向量共线的判断方法分析可得向量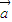
和
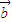共线的条件是m+n=4，由表可得
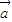和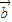
共线的情况数目，由等可能事件的概率公式，计算可得答案．
解答：解：根据题意，列表表示两次出现的点数情况：
共36种情况，
若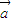
和
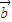共线，则有m-2=2-n，即m+n=4，有3种情况，
则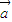
和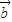
共线的概率为
=
；
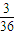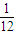故选B．
点评：本题考查等可能事件的概率计算、向量平行的坐标判断，注意关键是由向量共线的判断方法分析得到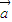
和
共线的情况数目．
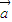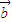和共线的条件是m+n=4，由表可得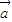和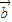共线的情况数目，由等可能事件的概率公式，计算可得答案．解答：解：根据题意，列表表示两次出现的点数情况：
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | （1，1） | （1，2） | （1，3） | （1，4） | （1，5） | （1，6） |
| 2 | （2，1） | （2，2） | （2，3） | （2，4） | （2，5） | （2，6） |
| 3 | （3，1） | （3，2） | （3，3） | （3，4） | （3，5） | （3，6） |
| 4 | （4，1） | （4，2） | （4，3） | （4，4） | （4，5） | （4，6） |
| 5 | （5，1） | （5，2） | （5，3） | （5，4） | （5，5） | （5，6） |
| 6 | （6，1） | （6，2） | （6，3） | （6，4） | （6，5） | （6，6） |
若
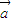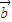和共线，则有m-2=2-n，即m+n=4，有3种情况，则
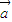和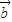共线的概率为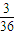=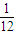；故选B．
点评：本题考查等可能事件的概率计算、向量平行的坐标判断，注意关键是由向量共线的判断方法分析得到
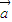和共线的情况数目． 
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
若将一颗质地均匀的骰子（一种各面上分别标有1，2，3，4，5，6个点的正方体玩具），先后抛掷两次，则出现向上的点数之和为4的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|