题目内容
5.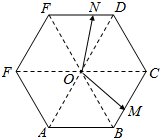 如图,正六边形ABCDEF的边长为1,O为其中心,M,N分别是BC,DE上的动点,且|$\overrightarrow{BM}$|=|$\overrightarrow{DN}$|.
如图,正六边形ABCDEF的边长为1,O为其中心,M,N分别是BC,DE上的动点,且|$\overrightarrow{BM}$|=|$\overrightarrow{DN}$|.(1)若M,N分别是BC,DE的中点,求$\overrightarrow{OM}$•$\overrightarrow{ON}$的值;
(2)求$\overrightarrow{OM}$•$\overrightarrow{ON}$的取值范围.
分析 (1)以O为原点,CF所在直线为x轴,建立如图所示的直角坐标系.求得C,B,D,E的坐标,由中点坐标公式可得M,N的坐标,再由数量积的坐标表示可得所求值;
(2)设|$\overrightarrow{BM}$|=|$\overrightarrow{DN}$|=t(0≤t≤1),则$\overrightarrow{BM}$=t$\overrightarrow{BC}$,$\overrightarrow{DN}$=t$\overrightarrow{DE}$,求得M,N的坐标,求得$\overrightarrow{OM}$•$\overrightarrow{ON}$的关于t的二次函数,再由对称轴和区间的关系,即可得到所求范围.
解答 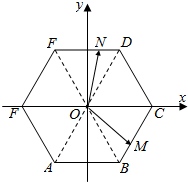 解:91)以O为原点,CF所在直线为x轴,建立如图所示的直角坐标系.
解:91)以O为原点,CF所在直线为x轴,建立如图所示的直角坐标系.
即有C(1,0),B($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),D(($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),E(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
M,N分别是BC,DE的中点,即有M($\frac{3}{4}$,-$\frac{\sqrt{3}}{4}$),N(0,$\frac{\sqrt{3}}{2}$),
则$\overrightarrow{OM}$•$\overrightarrow{ON}$=$\frac{3}{4}$×0+(-$\frac{\sqrt{3}}{4}$)×$\frac{\sqrt{3}}{2}$=-$\frac{3}{8}$;
(2)设|$\overrightarrow{BM}$|=|$\overrightarrow{DN}$|=t(0≤t≤1),
则$\overrightarrow{BM}$=t$\overrightarrow{BC}$,$\overrightarrow{DN}$=t$\overrightarrow{DE}$,
由(1)可得$\overrightarrow{BC}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{DE}$=(-1,0),
$\overrightarrow{OM}$=($\frac{1}{2}$t+$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$t-$\frac{\sqrt{3}}{2}$),$\overrightarrow{ON}$=(-t+$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
即有$\overrightarrow{OM}$•$\overrightarrow{ON}$=($\frac{1}{2}$t+$\frac{1}{2}$)($\frac{1}{2}$-t)+$\frac{\sqrt{3}}{2}$($\frac{\sqrt{3}}{2}$t-$\frac{\sqrt{3}}{2}$)
=$\frac{1}{2}$(t-t2-1)=-$\frac{1}{2}$(t-$\frac{1}{2}$)2-$\frac{3}{8}$,
由$\frac{1}{2}$∈[0,1],则t=$\frac{1}{2}$是,取得最大值-$\frac{3}{8}$;
t=0(或1)时,取得最小值-$\frac{1}{2}$.
则$\overrightarrow{OM}$•$\overrightarrow{ON}$的取值范围是[-$\frac{1}{2}$,-$\frac{3}{8}$].
点评 本题主要考查向量的数量积的坐标表示,考查化简整理的运算能力和二次函数的最值求法,注意坐标法思想的运用.

| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
| A. | [-1,$\frac{7}{5}$] | B. | [0,$\frac{7}{4}$] | C. | [-2,$\frac{7}{3}$] | D. | [-2,$\frac{7}{5}$] |
| A. | c≥0 | B. | c≤0 | ||
| C. | c不确定 | D. | 这样的函数f(x)不存在 |
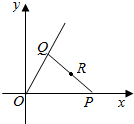 如图,已知P为x轴正半轴上的动点,Q为射线y=$\sqrt{3}$x(x>0)上的动点,△POQ的面积为8,求线段PQ的中心R的轨迹的参数方程.
如图,已知P为x轴正半轴上的动点,Q为射线y=$\sqrt{3}$x(x>0)上的动点,△POQ的面积为8,求线段PQ的中心R的轨迹的参数方程.