题目内容
4.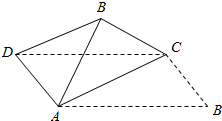 如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )
如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 设矩形纸片ABCD折起前B点为B1,连结BB1,DB1,由已知条件推导出BC⊥BD,BD=$\sqrt{2}$,BD⊥B1C,从而求出BB1,由DC∥AB1,得∠BAB1是异面直线AB和CD所成的角(或所成角的补角),由此利用余弦定理能求出异面直线AB和CD所成的角的余弦值.
解答 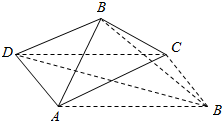 解:设矩形纸片ABCD折起前B点为B1,连结BB1,DB1,
解:设矩形纸片ABCD折起前B点为B1,连结BB1,DB1,
∵BC⊥AD,BC⊥AB,AB∩AD=A,
∴BC⊥平面ABD,∴BC⊥BD,
∵$AB=\sqrt{3}$,BC=1,∴BD=$\sqrt{3-1}$=$\sqrt{2}$,
∴AD2+BD2=AB2,∴AD⊥BD,∴BD⊥B1C,
∵BB1∩BC=B,∴BD⊥BB1,
∴BB1=$\sqrt{{B}_{1}{D}^{2}-B{D}^{2}}$=$\sqrt{1+3-2}$=$\sqrt{2}$,
∵DC∥AB1,∴∠BAB1是异面直线AB和CD所成的角(或所成角的补角),
cos∠BAB1=$\frac{A{B}^{2}+A{{B}_{1}}^{2}-B{{B}_{1}}^{2}}{2AB•A{B}_{1}}$=$\frac{3+3-2}{2×\sqrt{3}×\sqrt{3}}$=$\frac{2}{3}$.
∴异面直线AB和CD所成的角的余弦值为$\frac{2}{3}$.
故选:C.
点评 本题考查异面直线AB和CD所成的角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养和余弦定理的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.设${a_n}={n^2}-2kn+6$(n∈N*,k∈R)
(1)证明:k≤1是{an}为递增数列的充分不必要条件;
(2)若$?n∈{N^*},\frac{a_n}{n}≥1$,求k的取值范围.
(1)证明:k≤1是{an}为递增数列的充分不必要条件;
(2)若$?n∈{N^*},\frac{a_n}{n}≥1$,求k的取值范围.
9.甲、乙两人在相同条件下各射击10次,每次命中的环数如下:
(1)分别计算以上两组数据的平均数;
(2)分别计算以上两组数据的方差;
(3)根据计算结果,对甲乙两人的射击成绩作出评价.
( 参考公式:${s}^{2}=\frac{1}{n}$[${(x}_{1}-\overline{x})^{2}$+$({x}_{2}-\overline{x})^{2}$+…+$({x}_{n}-\overline{x})^{2}$])
| 甲 | 8 | 6 | 7 | 8 | 6 | 5 | 9 | 10 | 4 | 7 |
| 乙 | 6 | 7 | 7 | 8 | 6 | 7 | 8 | 7 | 9 | 5 |
(2)分别计算以上两组数据的方差;
(3)根据计算结果,对甲乙两人的射击成绩作出评价.
( 参考公式:${s}^{2}=\frac{1}{n}$[${(x}_{1}-\overline{x})^{2}$+$({x}_{2}-\overline{x})^{2}$+…+$({x}_{n}-\overline{x})^{2}$])
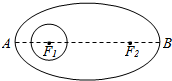 1998年12月19日,太原卫星发射中心为摩托罗拉公司(美国)发射了“铱星”系统通信卫星,卫星运行的轨道是椭圆,F1、F2是其焦点,地球中心为焦点F1,设地球半径为m,已知椭圆轨道的近地点A(离地面最近的点)距地面$\frac{m}{3}$,远地点B(离地面最远的点)距地面3m,并且F1、A、B在同一直线上,求卫星运行的轨道方程.
1998年12月19日,太原卫星发射中心为摩托罗拉公司(美国)发射了“铱星”系统通信卫星,卫星运行的轨道是椭圆,F1、F2是其焦点,地球中心为焦点F1,设地球半径为m,已知椭圆轨道的近地点A(离地面最近的点)距地面$\frac{m}{3}$,远地点B(离地面最远的点)距地面3m,并且F1、A、B在同一直线上,求卫星运行的轨道方程.