题目内容
(本题满分20分)设直线l1:y=k1x+1,l2:y=k2x-1,其中实数k1,k2满足k1k2+1=0.
(Ⅰ)证明:直线l1与l2相交;(Ⅱ)试用解析几何的方法证明:直线l1与l2的交点到原点距离为定值.(Ⅲ)设原点到l1与l2的距离分别为d1和d2求d1+d2的最大值
(Ⅰ)证明:直线l1与l2相交;(Ⅱ)试用解析几何的方法证明:直线l1与l2的交点到原点距离为定值.(Ⅲ)设原点到l1与l2的距离分别为d1和d2求d1+d2的最大值
(Ⅰ)反证法:假设l1与l2不相交,则l1与l2平行,有k1=k2,代入k1k2+1=0,得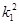 +2=1.此与k1为实数的事实相矛盾,从而k1≠k2,即l1与l2相交。(Ⅱ)由(Ⅰ)知
+2=1.此与k1为实数的事实相矛盾,从而k1≠k2,即l1与l2相交。(Ⅱ)由(Ⅰ)知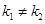 由方程组
由方程组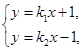 解得交点P的坐标(x,y)为
解得交点P的坐标(x,y)为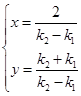 ,而x2+y2=
,而x2+y2=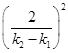 2+
2+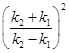 2=
2=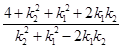 =
=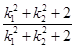 =1.即l1与l2的交点到原点距离为1
=1.即l1与l2的交点到原点距离为1
(Ⅲ)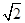
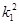 +2=1.此与k1为实数的事实相矛盾,从而k1≠k2,即l1与l2相交。(Ⅱ)由(Ⅰ)知
+2=1.此与k1为实数的事实相矛盾,从而k1≠k2,即l1与l2相交。(Ⅱ)由(Ⅰ)知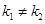 由方程组
由方程组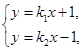 解得交点P的坐标(x,y)为
解得交点P的坐标(x,y)为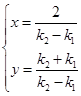 ,而x2+y2=
,而x2+y2=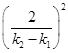 2+
2+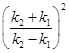 2=
2=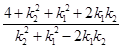 =
=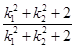 =1.即l1与l2的交点到原点距离为1
=1.即l1与l2的交点到原点距离为1(Ⅲ)
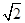
试题分析:(Ⅰ)反证法:假设l1与l2不相交,则l1与l2平行,有k1=k2,代入k1k2+1=0,得
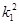 +2=1.此与k1为实数的事实相矛盾,从而k1≠k2,即l1与l2相交。
+2=1.此与k1为实数的事实相矛盾,从而k1≠k2,即l1与l2相交。(Ⅱ)方法一:由(Ⅰ)知
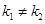 由方程组
由方程组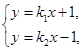
解得交点P的坐标(x,y)为
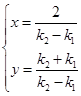
而x2+y2=
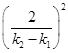 2+
2+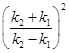 2=
2=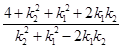 =
=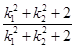 =1.
=1.即l1与l2的交点到原点距离为1
方法二:交点P的坐标(x,y)满足
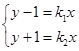 故知x≠0,从而
故知x≠0,从而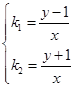
代入k1k2+1=0,得
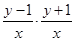 +1=0.整理后,得x2+y2=1得证。
+1=0.整理后,得x2+y2=1得证。(Ⅲ)方法一:
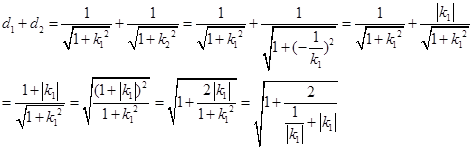
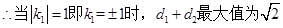
方法二:
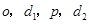 为矩形,
为矩形,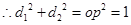
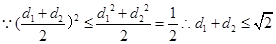 当且仅当
当且仅当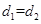 时取“=”
时取“=”
点评:关于两条直线位置关系的问题,常常单独出现在选择题和填空题中,或作为综合题的一部分出现在解答题中,主要考查以下三种:一、判断两条直线平行和垂直;二、求点到直线的距离、平行线间的距离;三、求直线的交点或夹角及利用它们求参数等

练习册系列答案
相关题目
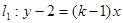 和直线
和直线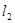 关于直线
关于直线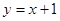 对称,那么直线
对称,那么直线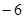 ,0),B(6,0),C(6,5),
,0),B(6,0),C(6,5),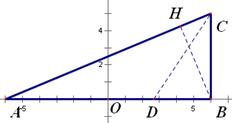
 的角平分线所在直线的方程。
的角平分线所在直线的方程。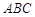 中,点
中,点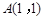 ,
,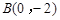 ,
,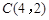 ,
,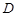 为
为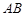 的中点,
的中点,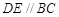 .
. 边上的高所在直线的方程;
边上的高所在直线的方程;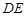 所在直线的方程.
所在直线的方程.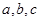 是
是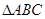 三个内角
三个内角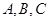 所对应的边,且
所对应的边,且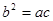 ,那么直线
,那么直线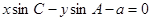 与直线
与直线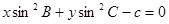 的位置关系
的位置关系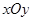 中,已知射线
中,已知射线 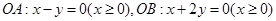 ,过点
,过点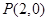 作直线分别交射线
作直线分别交射线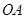 、
、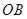 于点
于点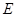 、
、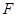 ,若
,若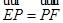 ,则直线
,则直线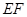 的斜率为
的斜率为 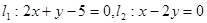
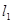 和直线
和直线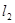 交点
交点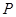 的坐标;
的坐标;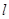 经过点
经过点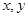 满足
满足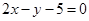 ,则
,则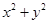 的最小值为________.
的最小值为________.