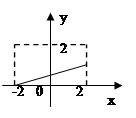题目内容
函数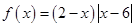 在
在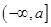 上取得最小值
上取得最小值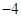 ,则实数
,则实数 的集合是( )
的集合是( )
A.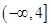 | B.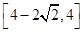 | C.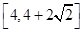 | D.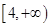 |
C
解析试题分析:由零点分段法,我们可将函数f(x)=(2-x)|x-6|的解析式化为分段函数的形式,然后根据分段函数分段处理的原则,画出函数的图象,进而结合图象数形结合,可得实数a的集合。解:因为函数
其函数图象如下图所示: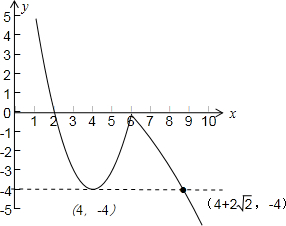
由函数图象可得:函数f(x)=(2-x)|x-6|在(-∞,a]上取得最小值-4时,实数a须满足4≤a≤4+2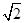 ,故实数a的集合是选C
,故实数a的集合是选C
考点:函数的最值
点评:本题考查的知识点是函数的最值及其几何意义,其中根据分段函数图象分段画的原则,画出函数的图象是解答本题的关键.

练习册系列答案
相关题目
设函数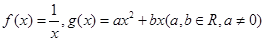 ,若
,若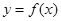 的图象与
的图象与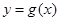 图象有且仅有两个不同的公共点
图象有且仅有两个不同的公共点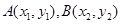 ,则下列判断正确的是( )
,则下列判断正确的是( )
A.当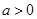 时, 时,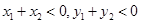 |
B.当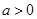 时, 时,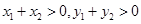 |
C.当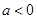 时, 时,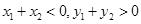 |
D.当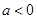 时, 时,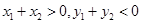 |
给右图的容器甲注水,下面图像中哪一个图像可以大致刻画容器中水的高度与时间的函数关系:( )。
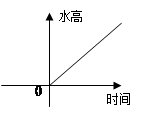
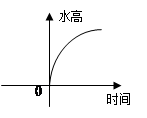
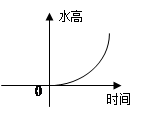

| A. | B. | C. | D. |
设函数 ,
, . 若当
. 若当 时,不等式
时,不等式 恒成立,则实数
恒成立,则实数 的取值范围是( ).
的取值范围是( ).
A. | B. | C. | D. |
设 是连续的偶函数,且当
是连续的偶函数,且当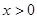 时,
时, 是单调函数,则满足
是单调函数,则满足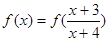 的所有
的所有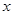 之和为( )
之和为( )
A.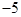 | B.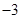 | C.5 | D.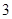 |
函数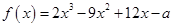 恰有两个不同的零点,则
恰有两个不同的零点,则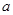 可以是( )
可以是( )
| A.3 | B.4 | C.6 | D.7 |
函数y=xlnx在区间 (0,1)上是 ( )
| A.单调增函数 |
| B.单调减函数 |
C.在(0,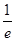 )上是减函数,在( )上是减函数,在(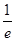 ,1)上是增函数 ,1)上是增函数 |
D.在(0,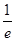 )上是增函数,在( )上是增函数,在(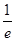 ,1)上是减函数 ,1)上是减函数 |
函数f(x)的定义域为R且满足:f(x)是偶函数,f(x-1)是奇函数,若f(0.5)=9则f(8.5)等于
| A.0 | B.9 | C.-3 | D.-9 |
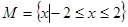 ,
, ,给出下列四个图形,其中能表示以M为定义域,N为值域的函数关系的是( )。
,给出下列四个图形,其中能表示以M为定义域,N为值域的函数关系的是( )。