Question

【题目】已知抛物线 的焦点为F,直线 与x轴的交点为P,与抛物线的交点为Q,且 .
（1）求抛物线的方程;
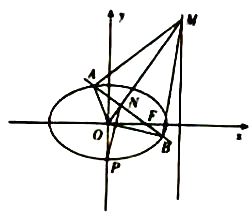
（2）过F的直线l与抛物线相交于A,D两点,与圆 相交于B,C两点(A,B两点相邻),过A,D两点分别作抛物线的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值.

Answer 1

【答案】
（1）解：由题意可知 ,由 ,则 ,解得 ，∴抛物线
（2）解：设 ，联立 ，整理得: ， 则 ，由 ，求导 ，直线 同理求得 ，则 ,解得: ,则 , 到 的距离 , 与 的面积之积为：
【解析】本题主要考查抛物线的标准方程，以及直线与圆锥曲线的位置关系，（1）根据题意求出QF，和p即可求出抛物线的方程。（2）设直线方程，然后联立直线方程和抛物线方程，利用韦达定理求出关系式，然后利用点到直线的距离公式求出高，进而求出面积的表达式即可。