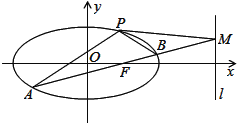
题目内容
【题目】.已知点![]() ,
,![]() ,动点
,动点![]() 满足条件
满足条件![]() .记动点
.记动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() 是
是![]() 上的不同两点,
上的不同两点,![]() 是坐标原点,求
是坐标原点,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据双曲线的定义可知轨迹为双曲线的右支,从而可得轨迹方程;(2)当直线![]() 斜率不存在时,可求得
斜率不存在时,可求得![]() ;当直线
;当直线![]() 斜率存在时,假设直线方程,代入
斜率存在时,假设直线方程,代入![]() 可整理得到一元二次方程;根据有两个正实根可构造出不等式组,求得斜率
可整理得到一元二次方程;根据有两个正实根可构造出不等式组,求得斜率![]() ;将
;将![]() 利用坐标运算表示为符合韦达定理的形式,代入整理后,结合
利用坐标运算表示为符合韦达定理的形式,代入整理后,结合![]() 可求得
可求得![]() ;综合两种情况可得所求最小值.
;综合两种情况可得所求最小值.
(1)![]()
![]() 由双曲线定义可知:点
由双曲线定义可知:点![]() 的轨迹是以
的轨迹是以![]() 为焦点的双曲线的右支
为焦点的双曲线的右支
![]()
![]() ,
,![]() ,
,![]()
![]() 的方程为:
的方程为:![]()
(2)①当直线![]() 斜率不存在时,设直线
斜率不存在时,设直线![]() 方程为:
方程为:![]()
此时![]() ,
,![]()
![]()
②当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() 方程为:
方程为:![]()
代入双曲线方程可得:![]()
可知上式有两个不等的正实数根![]()
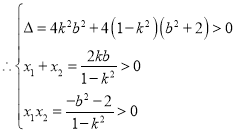
解得:![]()
![]()
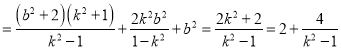
由![]() 得:
得:![]()
综上所述,![]() 的最小值为
的最小值为![]()

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
【题目】为了调查观众对电影“复仇者联盟4”结局的满意程度,研究人员在某电影院随机抽取了1000名观众作调查,所得结果如下所示,其中不喜欢“复仇者联盟4”的结局的观众占被调查观众总数的![]() .
.
男性观众 | 女性观众 | 总计 | |
喜欢“复仇者联盟4”的结局 | 400 | ||
不喜欢“复仇者联盟4”的结局 | 200 | ||
总计 |
(Ⅰ)完善上述![]() 列联表;
列联表;
(Ⅱ)是否有99.9%的把握认为观众对电影“复仇者联盟4”结局的满意程度与性别具有相关性?
附: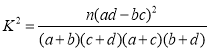
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |