题目内容
 单调函数,
单调函数,

 .
.(1)证明:f(0)=1且x<0时f(x)>1;
(2)
 (1)见解析(2)
(1)见解析(2)
本试题主要是考查了抽象函数性质的运用。
(1)在f(m+n)=f(m)·f(n)中,取m>0,n=0,有f(m)=f(m)·f(0) ,
∵x>0时0<f(x)<1 ∴f(0)=1
又设m=x<0,n=–x>0 则0<f(–x)<1
∴f(m+n)=" f(0)=" f(x)·f(–x)=1
∴f(x)= >1, 即x<0时,f(x)>1
>1, 即x<0时,f(x)>1
(2)
∴f(x)是定义域R上的单调递减函数
 ,然后解不等式得到。
,然后解不等式得到。
解析:(1)在f(m+n)=f(m)·f(n)中,取m>0,n=0,有f(m)=f(m)·f(0) ,
∵x>0时0<f(x)<1 ∴f(0)=1 ………3分
又设m=x<0,n=–x>0 则0<f(–x)<1
∴f(m+n)=" f(0)=" f(x)·f(–x)=1
∴f(x)= >1, 即x<0时,f(x)>1………6分
>1, 即x<0时,f(x)>1………6分
(2)
∴f(x)是定义域R上的单调递减函数. ………8分
 ………9分
………9分
 ………10分
………10分
 …11分
…11分
 ………13分
………13分
(1)在f(m+n)=f(m)·f(n)中,取m>0,n=0,有f(m)=f(m)·f(0) ,
∵x>0时0<f(x)<1 ∴f(0)=1
又设m=x<0,n=–x>0 则0<f(–x)<1
∴f(m+n)=" f(0)=" f(x)·f(–x)=1
∴f(x)=
 >1, 即x<0时,f(x)>1
>1, 即x<0时,f(x)>1(2)

∴f(x)是定义域R上的单调递减函数
 ,然后解不等式得到。
,然后解不等式得到。解析:(1)在f(m+n)=f(m)·f(n)中,取m>0,n=0,有f(m)=f(m)·f(0) ,
∵x>0时0<f(x)<1 ∴f(0)=1 ………3分
又设m=x<0,n=–x>0 则0<f(–x)<1
∴f(m+n)=" f(0)=" f(x)·f(–x)=1
∴f(x)=
 >1, 即x<0时,f(x)>1………6分
>1, 即x<0时,f(x)>1………6分(2)

∴f(x)是定义域R上的单调递减函数. ………8分
 ………9分
………9分 ………10分
………10分 …11分
…11分 ………13分
………13分
练习册系列答案
相关题目
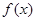 是二次函数,
是二次函数, 是它的导函数,且对任意的
是它的导函数,且对任意的 ,
, 恒成立.
恒成立. ,曲线
,曲线 :
: 在点
在点 处的切线为
处的切线为 ,
,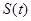 .求
.求 ,则使f(x)<0的x的取值范围为_____。
,则使f(x)<0的x的取值范围为_____。 满足
满足 。则
。则 =
=  ,对任意
,对任意 ,总有
,总有 ,则实数
,则实数 的最大整数值为( )
的最大整数值为( )



 在定义域R内可导,若
在定义域R内可导,若 ,且当
,且当 时,
时,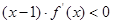 ,设a=f(0).b=
,设a=f(0).b= 则 ( )
则 ( ) ,
,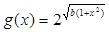 ,
, ,且
,且 ,
, .
. 、
、 的解析式;
的解析式;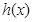 为定义在
为定义在 上的奇函数,且满足下列性质:①
上的奇函数,且满足下列性质:① 对一切实数
对一切实数 恒成立;②当
恒成立;②当 时
时 .
. 时,函数
时,函数 在区间
在区间 上的解的个数.
上的解的个数. ,
, ,其中
,其中 R.
R. 的单调性;
的单调性;
 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数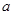 的取值范围;
的取值范围;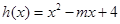 ,当
,当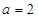 时,若
时,若 ,
, ,总有
,总有 成立,求实数
成立,求实数 的取值范围。
的取值范围。 则
则 ___________.
___________.