题目内容
已知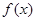 是二次函数,
是二次函数, 是它的导函数,且对任意的
是它的导函数,且对任意的 ,
, 恒成立.
恒成立.
(1)求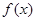 的解析表达式;
的解析表达式;
(2)设 ,曲线
,曲线 :
: 在点
在点 处的切线为
处的切线为 ,
, 与坐标轴围成的三角形面积为
与坐标轴围成的三角形面积为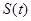 .求
.求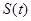 的最小值.
的最小值.
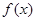 是二次函数,
是二次函数, 是它的导函数,且对任意的
是它的导函数,且对任意的 ,
, 恒成立.
恒成立.(1)求
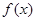 的解析表达式;
的解析表达式;(2)设
 ,曲线
,曲线 :
: 在点
在点 处的切线为
处的切线为 ,
, 与坐标轴围成的三角形面积为
与坐标轴围成的三角形面积为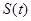 .求
.求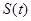 的最小值.
的最小值. (1)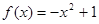 (2)
(2)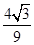
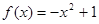 (2)
(2)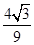
本题主要考查二次函数的概念、导数的应用等知识,以及运算求解能力.在解答过程当中,求导的能力、运算的能力、问题转换的能力以及数形结合的能力都得到了充分的体现,值得同学们体会反思.
(1)可以现设出二次函数的表达式,结合信息获得多项式相等进而利用对应系数相等解得参数,即可明确函数解析式;
(2)结合函数的解析式通过求导很容易求的在点P(t,f(t))处的切线l,由此即可表示出三角形的面积关于t的函数S(t).从而利用导函数知识即可求得函数S(t)的最小值
解:(Ⅰ)设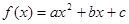 (其中
(其中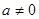 ),则
),则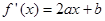 , ………1分
, ………1分
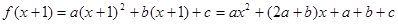 .
.
由已知,得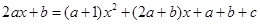 ,
,
∴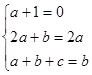 ,解之,得
,解之,得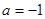 ,
,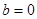 ,
,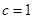 ,∴
,∴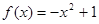 . ……4分
. ……4分
(2)由(1)得,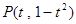 ,切线
,切线 的斜率
的斜率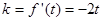 ,
,
∴切线 的方程为
的方程为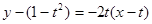 ,即
,即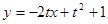 . …………6分
. …………6分
从而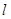 与
与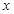 轴的交点为
轴的交点为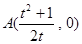 ,
,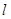 与
与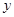 轴的交点为
轴的交点为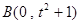 ,
,
∴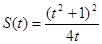 (其中
(其中 ). ………8分
). ………8分
∴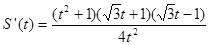 . ……………10分
. ……………10分
当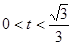 时,
时,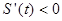 ,
,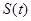 是减函数;
是减函数;
当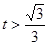 时,
时, ,
,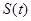 是增函数. ……12分
是增函数. ……12分
∴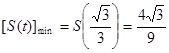 . …………13分
. …………13分
(1)可以现设出二次函数的表达式,结合信息获得多项式相等进而利用对应系数相等解得参数,即可明确函数解析式;
(2)结合函数的解析式通过求导很容易求的在点P(t,f(t))处的切线l,由此即可表示出三角形的面积关于t的函数S(t).从而利用导函数知识即可求得函数S(t)的最小值
解:(Ⅰ)设
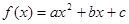 (其中
(其中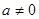 ),则
),则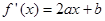 , ………1分
, ………1分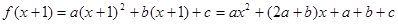 .
.由已知,得
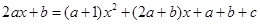 ,
,∴
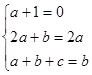 ,解之,得
,解之,得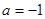 ,
,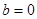 ,
,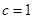 ,∴
,∴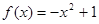 . ……4分
. ……4分(2)由(1)得,
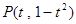 ,切线
,切线 的斜率
的斜率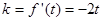 ,
,∴切线
 的方程为
的方程为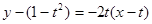 ,即
,即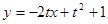 . …………6分
. …………6分从而
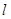 与
与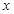 轴的交点为
轴的交点为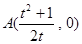 ,
,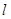 与
与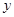 轴的交点为
轴的交点为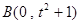 ,
,∴
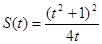 (其中
(其中 ). ………8分
). ………8分∴
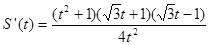 . ……………10分
. ……………10分当
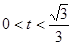 时,
时,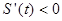 ,
,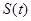 是减函数;
是减函数;当
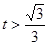 时,
时, ,
,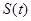 是增函数. ……12分
是增函数. ……12分∴
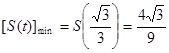 . …………13分
. …………13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 单调函数,
单调函数,

 .
. ,则
,则 的值为 .
的值为 . 在区间
在区间 上是减函数,在区间
上是减函数,在区间 上是增函数,则
上是增函数,则 _______.
_______. 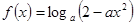 在
在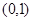 上为减函数,则实数
上为减函数,则实数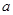 的取值范围是
的取值范围是



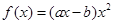 ,其中a、b为常数。
,其中a、b为常数。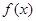 在点
在点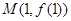 处的切线方程为
处的切线方程为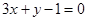 ,求a、b的值;
,求a、b的值;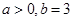 ,且函数
,且函数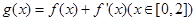 在
在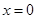 处取得最大值,求实数a的取值范围。
处取得最大值,求实数a的取值范围。 p、
p、 lnq万元,已知A、B两种型号的电视机的投放总额为10万元,且A、B两种型号的电视机的投放金额均不低于1万元,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出最大值(精确到0.1,参考数据:
lnq万元,已知A、B两种型号的电视机的投放总额为10万元,且A、B两种型号的电视机的投放金额均不低于1万元,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出最大值(精确到0.1,参考数据: ).
).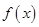 的图象经过点(4,2), 则下列命题正确的是( )
的图象经过点(4,2), 则下列命题正确的是( ) 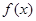 在R上满足
在R上满足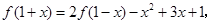 则曲线
则曲线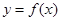 在点
在点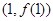 处的切线方程是 ( )
处的切线方程是 ( )