题目内容
【题目】已知抛物线
的焦点为
，点
为抛物线
上一点，且点
到焦点的距离为
.
（1）求拋物线的标准方程；
（2）设直线
在
轴上的截距为
，且与抛物线交于
，
两点，连接
并延长交抛物线的准线于点
，当直线
恰与抛物线相切时，求直线的方程.
【答案】（1）
；（2）
或
.
【解析】
（1）首先利用焦半径公式得到
，再写出抛物线方程即可.
（2）首先设直线
，
，
，联立直线与抛物线得到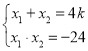
，利用导数求出在点
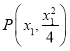处的切线方程，从而得到
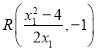，再根据
三点共线得到
，从而得到直线
的方程.
（1）由题知，
，所以
，解得，
故拋物线
的标准方程为.
（2）由题知，直线的斜率存在，不妨设直线，，.
由
，消y得
，即.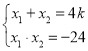
，
，
，
抛物线在点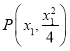处的切线方程为
.
令
，得
，
所以，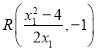
而三点共线，所以
及，得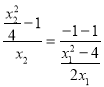
，
即
，
整理得
，
即：
，解得
，
即，
故所求直线的方程为或.
练习册系列答案
阅读快车系列答案
相关题目
【题目】某公司为了对某种商品进行合理定价，需了解该商品的月销售量
（单位：万件）与月销售单价
（单位：元/件）之间的关系，对近
个月的月销售量
和月销售单价
数据进行了统计分析，得到一组检测数据如表所示：
月销售单价 |
|
|
|
|
|
|
月销售量 |
|
|
|
|
|
|
（1）若用线性回归模型拟合与之间的关系，现有甲、乙、丙三位实习员工求得回归直线方程分别为：
，
和
，其中有且仅有一位实习员工的计算结果是正确的．请结合统计学的相关知识，判断哪位实习员工的计算结果是正确的，并说明理由；
（2）若用
模型拟合与之间的关系，可得回归方程为
，经计算该模型和（1）中正确的线性回归模型的相关指数
分别为
和
，请用说明哪个回归模型的拟合效果更好；
（3）已知该商品的月销售额为
（单位：万元），利用（2）中的结果回答问题：当月销售单价为何值时，商品的月销售额预报值最大？（精确到
）
参考数据：
.
