题目内容
【题目】在平面直角坐标![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为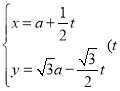 为参数,
为参数,![]() .在以坐标原点为极点、x轴的非负半轴为极轴的极坐标系中,曲线
.在以坐标原点为极点、x轴的非负半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若点![]() 在直线
在直线![]() 上,求直线
上,求直线![]() 的极坐标方程;
的极坐标方程;
(2)已知![]() ,若点
,若点![]() 在直线
在直线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,且
上,且![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)首先求出直线![]() 的直角坐标方程,将
的直角坐标方程,将![]() 代入求出
代入求出![]() ,再将直线的直角坐标方程化为极坐标方程即可.
,再将直线的直角坐标方程化为极坐标方程即可.
(2)首先求出曲线![]() 的参数方程,从而得到
的参数方程,从而得到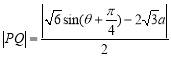 ,再根据
,再根据![]() 的最小值为
的最小值为![]() 即可得到
即可得到![]() 的值.
的值.
(1)直线![]() 的参数方程为
的参数方程为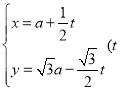 为参数,
为参数,![]() .
.
直角坐标方程为:![]() .
.
将![]() 代入
代入![]() ,解得
,解得![]() .
.
故直线![]() 的直角坐标方程为:
的直角坐标方程为:![]() ,
,
极坐标方程为:![]() .
.
(2)曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
转换为直角坐标方程为:![]() .
.
转换为参数方程为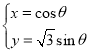 (
(![]() 为参数),
为参数),
直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
所以: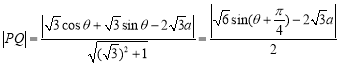 ,
,
所以当![]() 时,
时,![]() ,
,
解得:![]() .
.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目