题目内容
(本小题满分12分)设直线 与椭圆
与椭圆 相交于
相交于 两个不同的点,与
两个不同的点,与 轴相交于点
轴相交于点 ,记
,记 为坐标原点.
为坐标原点.
(1)证明:
(2)若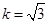 且
且 的面积及椭圆方程.
的面积及椭圆方程.
(1)根据直线与椭圆联立,结合判别式大于零来得到关系式。
(2)
解析试题分析:(1)证明:由  得
得 将
将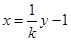 代入
代入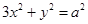 消去
消去 得
得 ① ………………………… 2分
① ………………………… 2分
由直线l与椭圆相交于两个不同的点得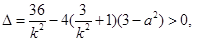 整理得
整理得 ,即
,即 ……4分
……4分
(2)解:设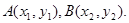 ①为
①为
得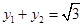
∵ 而点
而点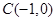 , ∴
, ∴
得 代入上式,得
代入上式,得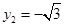 ……………7分
……………7分
于是,△OAB的面积 
 --------10分
--------10分
将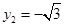 代入
代入 ,可解出
,可解出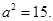
∴△OAB的面积为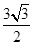 椭圆方程是
椭圆方程是 ……………12分
……………12分
考点:本试题考查了直线与椭圆的位置关系的运用。
点评:解决该试题的关键是通过联立方程组,得到二次方程中判别式大于零,得到证明。同时要结合向量的坐标关系,以及根与系数的关系,解得坐标,求解面积和椭圆方程。属于中档题。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
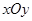 中,以
中,以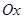 轴为始边作两个锐角
轴为始边作两个锐角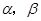 ,它们的终边分别交单位圆于
,它们的终边分别交单位圆于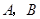 两点.已知
两点.已知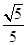 ,
,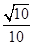 .
.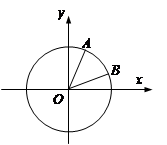
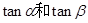 的值;(2)求
的值;(2)求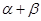 的值.
的值.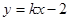 相交于不同的两点A、B,且AB中点横坐标为2,求k的值.
相交于不同的两点A、B,且AB中点横坐标为2,求k的值.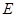 :
: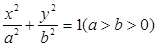 的右焦点
的右焦点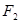 与抛物线
与抛物线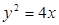 的焦点重合,过
的焦点重合,过 轴垂直的直线
轴垂直的直线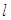 与椭圆交于
与椭圆交于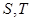 两点,与抛物线交于
两点,与抛物线交于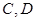 两点,且
两点,且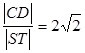 。
。 的直线与椭圆
的直线与椭圆 ,设
,设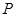 为椭圆
为椭圆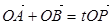
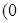 为坐标原点),当
为坐标原点),当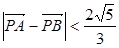 时,求实数
时,求实数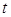 的取值范围。
的取值范围。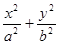 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为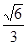 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为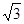 .
.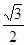 ,求△AOB面积的最大值.
,求△AOB面积的最大值. ,焦点在
,焦点在 轴上,两条渐近线分别为
轴上,两条渐近线分别为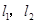 ,经过右焦点
,经过右焦点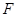 垂直于
垂直于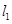 的直线分别交
的直线分别交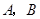 两点.已知
两点.已知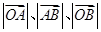 成等差数列,且
成等差数列,且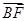 与
与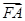 同向.
同向.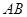 被双曲线所截得的线段的长为4,求双曲线的方程.
被双曲线所截得的线段的长为4,求双曲线的方程.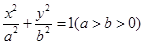 的两个焦点为
的两个焦点为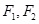 ,椭圆的离心率为
,椭圆的离心率为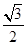 ,
, 点是椭圆上任意一点, 且
点是椭圆上任意一点, 且 ,
,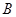 为直角顶点作椭圆的内接等腰直角三角形
为直角顶点作椭圆的内接等腰直角三角形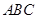 ,这样的等腰直角三角形是否存在?若存在请说明有几个、并求出直角边所在直线方程?若不存在,请说明理由.
,这样的等腰直角三角形是否存在?若存在请说明有几个、并求出直角边所在直线方程?若不存在,请说明理由.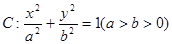 的离心率为
的离心率为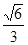 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6。
,椭圆C上任意一点到椭圆两个焦点的距离之和为6。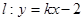 与椭圆C交于A、B两点,点P(0,1),且|PA|=|PB|,求直线
与椭圆C交于A、B两点,点P(0,1),且|PA|=|PB|,求直线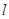 的方程。
的方程。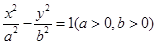 的一个焦点,并与双曲线的实轴垂直,已知抛物线与双曲线的交点为
的一个焦点,并与双曲线的实轴垂直,已知抛物线与双曲线的交点为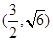 .
.