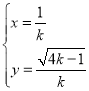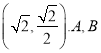题目内容
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,右顶点为
,右顶点为![]() ,且
,且![]() 过点
过点![]() ,圆
,圆![]() 是以线段
是以线段![]() 为直径的圆,经过点
为直径的圆,经过点![]() 且倾斜角为
且倾斜角为![]() 的直线与圆
的直线与圆![]() 相切.
相切.
(1)求椭圆![]() 及圆
及圆![]() 的方程;
的方程;
(2)是否存在直线![]() ,使得直线
,使得直线![]() 与圆
与圆![]() 相切,与椭圆
相切,与椭圆![]() 交于
交于![]() 两点,且满足
两点,且满足![]() ?若存在,请求出直线
?若存在,请求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
【答案】(1)椭圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ;(2)不存在
;(2)不存在
【解析】分析:(1)由题意得![]() ,再根据椭圆过点
,再根据椭圆过点![]() 得到关于
得到关于![]() 的方程组,求解后可得椭圆和圆的方程.(2)先假设存在直线满足条件.(ⅰ)当直线斜率不存在时,可得直线方程为
的方程组,求解后可得椭圆和圆的方程.(2)先假设存在直线满足条件.(ⅰ)当直线斜率不存在时,可得直线方程为![]() ,求得点
,求得点![]() 的坐标后验证可得
的坐标后验证可得![]() ;(ⅱ)当直线斜率存在时,设出直线方程,与椭圆方程联立消元后得到一元二次方程,结合根据系数的关系可得
;(ⅱ)当直线斜率存在时,设出直线方程,与椭圆方程联立消元后得到一元二次方程,结合根据系数的关系可得
![]() 不成立.从而可得不存在直线
不成立.从而可得不存在直线![]() 满足题意.
满足题意.
详解:(1)由题意知![]() ,
,![]() ,
,![]() ,圆
,圆![]() 的方程为
的方程为![]()
由题可知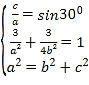 ,解得
,解得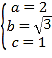 ,
,
所以椭圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() .
.
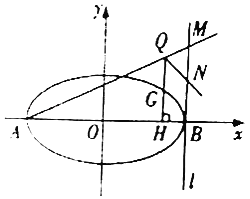
(2)假设存在直线![]() 满足题意.
满足题意.
由![]() ,可得
,可得![]() ,故
,故![]() .
.
(ⅰ)当直线![]() 的斜率不存在时,此时
的斜率不存在时,此时![]() 的方程为
的方程为![]() .
.
当直线![]() 时,可得
时,可得![]()
所以![]() .
.
同理可得,当![]() 时,
时,![]() .
.
故直线![]() 不存在.
不存在.
(ⅱ)当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 方程为
方程为![]() ,
,
因为直线![]() 与圆
与圆![]() 相切,
相切,
所以![]() ,整理得
,整理得![]() ①
①
由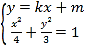 消去y整理得
消去y整理得![]() ,
,
设![]() ,
,
则![]() ,
,![]() ,
,
因为![]() ,
,
所以![]() ,
,
则![]() ,即
,即![]() ,
,
所以![]() ,
,
所以![]() ,
,
整理得![]() ②
②
由①②得![]() ,此时方程无解.
,此时方程无解.
故直线![]() 不存在.
不存在.
由(i)(ii)可知不存在直线![]() 满足题意.
满足题意.

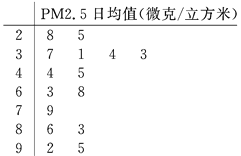
【题目】空气质量指数AQI是一种反映和评价空气质量的方法,AQI指数与空气质量对应如表所示:
AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某城市2018年12月全月的AQI指数变化统计图:

根据统计图判断,下列结论正确的是( )
A. 整体上看,这个月的空气质量越来越差
B. 整体上看,前半月的空气质量好于后半个月的空气质量
C. 从AQI数据看,前半月的方差大于后半月的方差
D. 从AQI数据看,前半月的平均值小于后半月的平均值