题目内容
14.有下列4个命题:①两个平面垂直,过一个平面内任意一点作交线的垂线,则此直线必垂直于另一平面;
②平面α内两条不平行的直线都平行于另一平面β,则α∥β;
③两条直线和一个平面所成的角相等,则这两条直线平行;
④直线a不平行于平面α,则平面α内不存在与直线a平行的直线.
其中正确命题的个数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 通过举反例,得到①③④都是错误命题,利用平面与平面平行的判定定理,得到②是正确命题.
解答 解:在①中:两个平面垂直,过一个平面内任意一点作交线的垂线,则此直线不一定垂直于另一平面,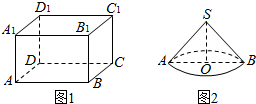
举反例:以图1中的长方体为例,平面ABB1A1⊥平面ABCD,交线为AB,
点B∈平面ABB1A1,BC1⊥AB,但BC1不垂直于平面ABCD,故①错误;
在②中:平面α内两条不平行的直线都平行于另一平面β,根据平面与平面平行的判定定理,得②正确;
在③中:两条直线和一个平面所成的角相等,则这两条直线不一定平行,
举反例:图2的圆锥中,SA,SB与底面所在平面所成的角相等,但SA与SB不平行,故③错误;
在④中:直线a不平行于平面α,则平面α内有可能存在与直线a平行的直线,
举反例:当直线a?平面α时,平面α内存在与直线a平行的直线,故④错误.
故选:D.
点评 本题考查命题真假的判断,是中档题,解题时要注意空间中直线与直线、直线与平面、平面与平面位置关系的合理运用.

练习册系列答案
相关题目
5.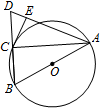 如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E,若AB=8,DC=4,则DE=( )
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E,若AB=8,DC=4,则DE=( )
 如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E,若AB=8,DC=4,则DE=( )
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E,若AB=8,DC=4,则DE=( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{4}{3}$ |
6.已知两定点A(-2,1),B(1,3),动点P在直线x-y+1=0上,当|PA|+|PB|取最小值时,这个最小值为( )
| A. | $\sqrt{5}$ | B. | 3 | C. | $\sqrt{13}$ | D. | $\sqrt{17}$ |
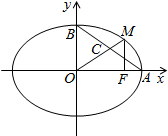 (Ⅰ)求过点($\sqrt{3},2\sqrt{2}$)且与双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$有相同渐近线的双曲线的标准方程.
(Ⅰ)求过点($\sqrt{3},2\sqrt{2}$)且与双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$有相同渐近线的双曲线的标准方程.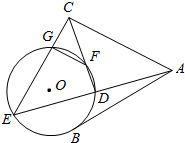 如图,AB是⊙O的一条切线,切点为B,ADE,CFD和 CGE都是⊙O的割线,AC=AB
如图,AB是⊙O的一条切线,切点为B,ADE,CFD和 CGE都是⊙O的割线,AC=AB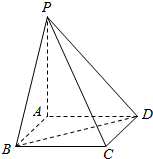 已知PA垂直于矩形ABCD所在平面,PA=3,AB=1,BC=$\sqrt{3}$.
已知PA垂直于矩形ABCD所在平面,PA=3,AB=1,BC=$\sqrt{3}$.