题目内容
 在第十六届广州亚运会上,某项目的比赛规则为:由两人(记为甲和乙)进行比赛,每局胜者得1分,负者得0分(无平局),比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为p(p>0.5),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
在第十六届广州亚运会上,某项目的比赛规则为:由两人(记为甲和乙)进行比赛,每局胜者得1分,负者得0分(无平局),比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为p(p>0.5),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为| 5 | 9 |
(Ⅰ)求实数p的值;
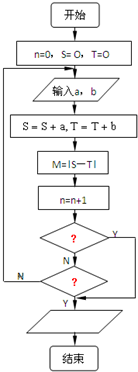
(Ⅱ)如图为统计比赛的局数n和甲、乙的总得分数S、T的程序框图.其中如果甲获胜,输入a=1,b=0;如果乙获胜,则输入a=0,b=1.请问在第一、第二两个判断框中应分别填写什么条件;
(Ⅲ)设ζ表示比赛停止时已比赛的局数,求随机变量ζ的分布列和数学期望Eζ.
分析:(Ⅰ)依题意,当甲连胜2局或乙连胜2局时,第二局比赛结束时比赛结束,又知第二局比赛结束时比赛停止的概率为
,用P表示出第二局比赛结束的概率,使它等于
解出结果.
(Ⅱ)从框图知,这是一个含有两个条件的框图,结合题目所给的条件,程序框图中的第一个条件框应填M=2,第二个应填n=6.
(Ⅲ)依题意知,ξ的所有可能值为2,4,6.设每两局比赛为一轮,则该轮结束时比赛停止的概率为
.若该轮结束时比赛还将继续,则甲、乙在该轮中必是各得一分,该轮比赛结果对下轮比赛是否停止没有影响.写出分布列和期望.
| 5 |
| 9 |
| 5 |
| 9 |
(Ⅱ)从框图知,这是一个含有两个条件的框图,结合题目所给的条件,程序框图中的第一个条件框应填M=2,第二个应填n=6.
(Ⅲ)依题意知,ξ的所有可能值为2,4,6.设每两局比赛为一轮,则该轮结束时比赛停止的概率为
| 5 |
| 9 |
解答:解:(Ⅰ)依题意,当甲连胜2局或乙连胜2局时,第二局比赛结束时比赛结束.
有p2+(1-p)2=
.…(2分)
解得p=
或p=
.…(3分)
∵p>
,∴p=
.…(4分)
(Ⅱ)程序框图中的第一个条件框应填M=2,第二个应填n=6.…(8分)
注意:答案不唯一. 如:第一个条件框填M>1,第二个条件框填n>5,或者第一、第二条件互换,都可以.
(Ⅲ)依题意知,ζ的所有可能值为2,4,6. …(9分)
由已知 P(ξ=2)=
,P(ξ=4)=
p3(1-p)+
(1-p)3p=
P(ξ=6)=1-P(ξ=2)-P(ξ=4)=
.…(11分)
∴随机变量ζ的分布列为:
故Eξ=2×
+4×
+6×
=
.…(12分)
有p2+(1-p)2=
| 5 |
| 9 |
解得p=
| 2 |
| 3 |
| 1 |
| 3 |
∵p>
| 1 |
| 2 |
| 2 |
| 3 |
(Ⅱ)程序框图中的第一个条件框应填M=2,第二个应填n=6.…(8分)
注意:答案不唯一. 如:第一个条件框填M>1,第二个条件框填n>5,或者第一、第二条件互换,都可以.
(Ⅲ)依题意知,ζ的所有可能值为2,4,6. …(9分)
由已知 P(ξ=2)=
| 5 |
| 9 |
| C | 1 2 |
| C | 1 2 |
| 20 |
| 81 |
P(ξ=6)=1-P(ξ=2)-P(ξ=4)=
| 16 |
| 81 |
∴随机变量ζ的分布列为:
| ζ | 2 | 4 | 6 | ||||||
| P |
|
|
|
| 5 |
| 9 |
| 20 |
| 81 |
| 16 |
| 81 |
| 266 |
| 81 |
点评:本题考查概率知识,考查流程图,考查离散型随机变量的分布列与期望,解题的关键是确定变量的取值与含义,正确求概率.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
(本小题12分)第十六届亚运会将于2010年11月12日至27日在中国广州进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男女志愿者中分别有10人和6人喜爱运动,其余不喜爱。
| 喜爱运动 | 不喜爱运动 | 合计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 合计 | 30 |
(1)根据以上数据完成下面列联表:
(2)根据列联表的独立性检验,能否有![]() 把握认为性别与喜爱运动有关。
把握认为性别与喜爱运动有关。
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考公式: ![]()
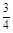 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是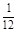 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是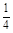 .
.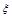 的分布列和期望.
的分布列和期望.