题目内容
2010年11月广州成功举办了第十六届亚运会.在华南理工大学学生会举行的亚运知识有奖问答比赛中,甲、乙、丙同时回答一道有关亚运知识的问题,已知甲回答对这道题目的概率是
,甲、丙两人都回答错的概率是
,乙、丙两人都回答对的概率是
.
(1)求乙、丙两人各自回答对这道题目的概率.
(2)求回答对这道题目的人数的随机变量ξ的分布列和期望.
| 3 |
| 4 |
| 1 |
| 12 |
| 1 |
| 4 |
(1)求乙、丙两人各自回答对这道题目的概率.
(2)求回答对这道题目的人数的随机变量ξ的分布列和期望.
分析:(1)设乙、丙各自回答对的概率分别是p1,p2,根据题意,得
,由此能求出乙、丙两人各自回答对这道题目的概率.
(2)ξ可能取值0,1,2,3,分别求出P(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),由此能求出ξ的分布列和数学期望为Eξ.
|
(2)ξ可能取值0,1,2,3,分别求出P(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),由此能求出ξ的分布列和数学期望为Eξ.
解答:解:(1)设乙、丙各自回答对的概率分别是p1,p2,
根据题意,得
,
解得p1 =
,p2=
.
故乙答对的概率为
,丙答对的概率为
.
(2)ξ可能取值0,1,2,3,
P(ξ=0)=
×
×
=
;
P(ξ=1)=
=
;
P(ξ=2)=
=
;
P(ξ=3)=
=
.
∴ξ的分布列如下:
数学期望为Eξ=
×0+
×1+
×2+
×3=
.
根据题意,得
|
解得p1 =
| 3 |
| 8 |
| 2 |
| 3 |
故乙答对的概率为
| 3 |
| 8 |
| 2 |
| 3 |
(2)ξ可能取值0,1,2,3,
P(ξ=0)=
| 1 |
| 4 |
| 5 |
| 8 |
| 1 |
| 3 |
| 5 |
| 96 |
P(ξ=1)=
| 3×5×1+1×3×1+1×5×2 |
| 96 |
| 28 |
| 96 |
P(ξ=2)=
| 3×3×1+3×5×2+1×3×2 |
| 96 |
| 45 |
| 96 |
P(ξ=3)=
| 3×3×2 |
| 96 |
| 18 |
| 96 |
∴ξ的分布列如下:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| p |
|
|
|
|
| 5 |
| 96 |
| 7 |
| 24 |
| 15 |
| 32 |
| 3 |
| 16 |
| 43 |
| 24 |
点评:本题考查离散型随机变量的分布列和数学期望,是中档题,在历年高考中都是必考题型,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
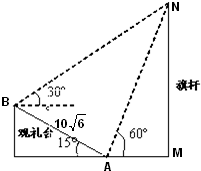 2010年11月12日广州亚运会上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和30°,且座位A、B的距离为
2010年11月12日广州亚运会上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和30°,且座位A、B的距离为 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是 .
.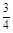 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是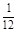 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是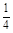 .
.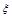 的分布列和期望.
的分布列和期望.