题目内容
第十六届亚运会将于2010年11月12日至27日在中国广州进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男女志愿者中分别有10人和6人喜爱运动,其余不喜爱.
(1)根据以上数据完成下面列联表:
(2)根据列联表的独立性检验,能否有90%把握认为性别与喜爱运动有关.
参考公式:K2=
.
| 喜爱运动 | 不喜爱运动 | 合计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 合计 | 30 |
(2)根据列联表的独立性检验,能否有90%把握认为性别与喜爱运动有关.
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
分析:(1)本题是一个简单的数字的运算,根据a,b,c,d的已知和未知的结果,做出空格处的结果.
(2)假设是否喜爱运动与性别无关,由已知数据可求得观测值,把求得的观测值同临界值进行比较,看能否有90%把握认为性别与喜爱运动有关.
(2)假设是否喜爱运动与性别无关,由已知数据可求得观测值,把求得的观测值同临界值进行比较,看能否有90%把握认为性别与喜爱运动有关.
解答:解:(1)根据条件中所给的a,b,c,d,a+b,a+d,c+d,b+d的值,利用实数的加减运算得到列联表:
(2)假设:是否喜爱运动与性别无关,由已知数据可求得:
K2=
≈1.1575<2.706,
因此,在犯错的概率不超过0.10的前提下不能判断喜爱运动与性别有关,
故不能得到有90%把握认为性别与喜爱运动有关.
| 喜爱运动 | 不喜爱运动 | 合计 | |
| 男 | 10 | 6 | 16 |
| 女 | 6 | 8 | 14 |
| 合计 | 16 | 14 | 30 |
K2=
| 30×(10×8-6×6)2 |
| (10+6)(6+8)(10+6)(6+8) |
因此,在犯错的概率不超过0.10的前提下不能判断喜爱运动与性别有关,
故不能得到有90%把握认为性别与喜爱运动有关.
点评:本题考查独立性检验的列联表.考查假设性判断,解题的过程比较麻烦,但这种问题的解答原理比较简单,是一个送分题目.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
第十六届亚运会将于2010年11月12日至27日在中国广州进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男女志愿者中分别有10人和6人喜爱运动,其余不喜爱.
| 喜爱运动 | 不喜爱运动 | 合计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 合计 | 30 |
(2)根据列联表的独立性检验,能否有90%把握认为性别与喜爱运动有关.
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
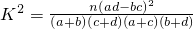 .
. (本小题12分)第十六届亚运会将于2010年11月12日至27日在中国广州进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男女志愿者中分别有10人和6人喜爱运动,其余不喜爱。
| 喜爱运动 | 不喜爱运动 | 合计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 合计 | 30 |
(1)根据以上数据完成下面列联表:
(2)根据列联表的独立性检验,能否有![]() 把握认为性别与喜爱运动有关。
把握认为性别与喜爱运动有关。
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考公式: ![]()
第十六届亚运会将于2010年11月12日至27日在中国广州进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男女志愿者中分别有10人和6人喜爱运动,其余不喜爱.
(1)根据以上数据完成下面列联表:
(2)根据列联表的独立性检验,能否有90%把握认为性别与喜爱运动有关.
参考公式: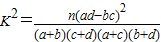 .
.
| 喜爱运动 | 不喜爱运动 | 合计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 合计 | 30 |
(2)根据列联表的独立性检验,能否有90%把握认为性别与喜爱运动有关.
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
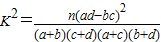 .
.