题目内容
9.若f(x)=x2-x+b,且f(log2a)=b,log2|f(a)|=2(a≠1),当满足log2(2-x)≤2时,求f(2x)的最小值及对应的x值.分析 由f(log2a)=b可求出a,再由log2f(a)=2即可求得b,从而求出解析式;表示出f (2x),配方后利用函数单调性可求最小值及x值.
解答 解:(1)由f(log2a)=b,得(log2a)2-log2a+b=b,即(log2a)2-log2a=0,
解得log2a=1或log2a=0(舍),所以a=2.
由log2|f(a)|=2,得f(a)=±4,即f(2)=±4,
所以22-2+b=±4,解得b=2或者b=-6.
所以函数f(x)=x2-x+2或者f(x)=x2-x-6;当满足log2(2-x)≤2时,即-2≤x≤2时,$\frac{1}{4}$≤2x≤4,所以f(2x)=(2x)2-2x+2=(2x-$\frac{1}{2}$)2+$\frac{7}{4}$,当x=-1时,f(2x)的最小值为$\frac{7}{4}$;
或者f(2x)=(2x)2-2x-6=(2x-$\frac{1}{2}$)2-$\frac{25}{4}$,当x=-1时最小值为-$\frac{25}{4}$.
点评 本题考查复合函数的单调性及二次函数的性质,属中档题

练习册系列答案
相关题目
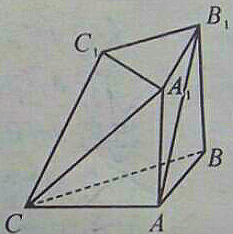 如图在多面体ABC-A1B1C1中,AA1$\underset{∥}{=}$BB1,B1C1$\underset{∥}{=}$$\frac{1}{2}$BC,求证:AB1∥平面 A1C1C.
如图在多面体ABC-A1B1C1中,AA1$\underset{∥}{=}$BB1,B1C1$\underset{∥}{=}$$\frac{1}{2}$BC,求证:AB1∥平面 A1C1C.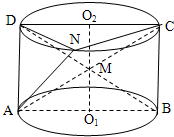 如图,已知矩形ABCD是圆柱O1O2的轴截面,N在上底面的圆周O2上,AC,BD相交于点M.
如图,已知矩形ABCD是圆柱O1O2的轴截面,N在上底面的圆周O2上,AC,BD相交于点M.