题目内容
【题目】将边长为![]() 的正三角形利用平行于边的直线剖分为
的正三角形利用平行于边的直线剖分为![]() 个边长为1的小正三角形.图3为
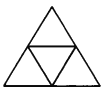
个边长为1的小正三角形.图3为![]() 的情形.证明:存在正整数
的情形.证明:存在正整数![]() ,使得小三角形的顶点中可选出2000
,使得小三角形的顶点中可选出2000![]() 个点,其中,任意三点均不构成正三角形.
个点,其中,任意三点均不构成正三角形.
【答案】见解析
【解析】
首先证明一个引理.
引理 若边长为![]() 的正三角形内部(不含边界)可选出
的正三角形内部(不含边界)可选出![]() 个点(而不构成三角形),则边长为3
个点(而不构成三角形),则边长为3![]() 的正三角形可选出4
的正三角形可选出4![]() 个点.
个点.
证明 事实上,边长3![]() 的正三角形可分为9个边长
的正三角形可分为9个边长![]() 的正三角形,如图1,其中,4个(编号1、2、3、4)分别可选出
的正三角形,如图1,其中,4个(编号1、2、3、4)分别可选出![]() 个点(不构成正三角形).
个点(不构成正三角形).
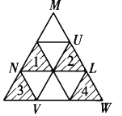
图1
下面证明:这4![]() 个点一起也不构成正三角形.任取其中三点
个点一起也不构成正三角形.任取其中三点![]() .
.
【情形1】
三点![]() 在同一编号的三角形内.
在同一编号的三角形内.
据该三角形内![]() 个点的选取方式,故点
个点的选取方式,故点![]() 不构成三角形.
不构成三角形.
【情形2】
两点(不妨设![]() )在同一编号三角形,另一点在其余编号三角形内.
)在同一编号三角形,另一点在其余编号三角形内.
考虑含![]() 两点的三角形,如图2.据平面几何知识,知与
两点的三角形,如图2.据平面几何知识,知与![]() 形成正三角形的第三个顶点应在一个“大三角形”内,该大三角形以
形成正三角形的第三个顶点应在一个“大三角形”内,该大三角形以![]() 为中位三角形.图1中每个编号的三角形的大三角形与其余编号的三角形并无交集.故点
为中位三角形.图1中每个编号的三角形的大三角形与其余编号的三角形并无交集.故点![]() 不构成正三角形.
不构成正三角形.
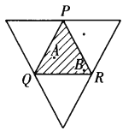
图2
【情形3】
每个点在不同编号的三角形内.
据对称性,只需考虑编号为1、2、4或2、3、4两种.
前一种,不妨设点![]() 分别在编号1、2、4三角形内.则
分别在编号1、2、4三角形内.则![]() 两点均在
两点均在![]() ,但以
,但以![]() 为中位三角形的大三角形与编号4的三角形并无交集.
为中位三角形的大三角形与编号4的三角形并无交集.
后一种,不妨设点![]() 分别在编号2、3、4三角形内.则
分别在编号2、3、4三角形内.则![]() 两点均在
两点均在![]() 内,但以
内,但以![]() 为中位三角形的大三角形与编号3的三角形并无交集.
为中位三角形的大三角形与编号3的三角形并无交集.
于是,两种类型均有点![]() 不构成正三角形.
不构成正三角形.
综合以上三种情形,引理得证.
如图,边长为3的正三角形内部(不含边界)可选出一个点(而不形成正三角形).用上述结论,可归纳证明:边长为![]() 的三角形内(不含边界)可选出
的三角形内(不含边界)可选出![]() 个点(而不构成正三角形).
个点(而不构成正三角形).
只要证明:存在![]() ,使得
,使得![]() .
.
由![]() ,知存在
,知存在![]() ,使得
,使得![]() .
.
从而,![]() .
.
令![]() 即得.
即得.

练习册系列答案
相关题目