题目内容
已知函数f(x)=ex+4x-3.(Ⅰ)求证函数f(x)在区间[0,1]上存在唯一的零点,并用二分法求函数f(x)零点的近似值(误差不超过0.2);(参考数据e≈2.7,
| e |
(Ⅱ)当x≥1时,若关于x的不等式f(x)≥ax恒成立,试求实数a的取值范围.
分析:对第(Ⅰ)问要先根据题意判断函数在相应区间上的单调性,再有端点的函数值对比即可获得解的唯一性,然后再根据二分法的步骤逐次进行范围缩小,再结合所给信息即可获得问题的解答;
对第(Ⅱ)首先将恒成立问题游离参数,转化为求函数g(x)=
的最小值问题即可.
对第(Ⅱ)首先将恒成立问题游离参数,转化为求函数g(x)=
| ex+4x-3 |
| x |
解答:解:(Ⅰ)由f(x)=ex+4x-3,得f′(x)=ex+4>0,
f(x)在[0,1]上单调递增,
∵f(0)=-2,f(1)=e+1>0,f(0)•f(1)<00,
∴f(x)在[0,1]上存在唯一零点,
取区间[0,1]作为起始区间,用二分法逐次计算如下
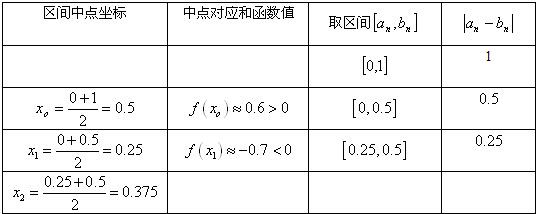
由上表可知区间[0.25,0.5]的长度为0.25,所以该区间的中点x2=0.375,到区间端点距离小于0.2,因此可作为误差不超过0.2的一个零点的近似值.
∴函数f(x)零点的近似值x≈0.375
(Ⅱ)当x≥1时,由f(x)≥ax,即a≤
,
令g(x)=
则g′(x)=
∵x≥1,
∴g′(x)>0,
∴g(x)在[1,+∞)上单调递增,
∴g(x)min=g(1)=e+1,
∴a的取值范围是a≤e+1.
f(x)在[0,1]上单调递增,
∵f(0)=-2,f(1)=e+1>0,f(0)•f(1)<00,
∴f(x)在[0,1]上存在唯一零点,
取区间[0,1]作为起始区间,用二分法逐次计算如下

由上表可知区间[0.25,0.5]的长度为0.25,所以该区间的中点x2=0.375,到区间端点距离小于0.2,因此可作为误差不超过0.2的一个零点的近似值.
∴函数f(x)零点的近似值x≈0.375
(Ⅱ)当x≥1时,由f(x)≥ax,即a≤
| ex+4x-3 |
| x |
令g(x)=
| ex+4x-3 |
| x |
| ex(x-1)+3 |
| x2 |
∵x≥1,
∴g′(x)>0,
∴g(x)在[1,+∞)上单调递增,
∴g(x)min=g(1)=e+1,
∴a的取值范围是a≤e+1.
点评:此题考查的是二分法求方程的近似解和恒成立的综合类问题.在解答的过程当中充分体现了数形结合的思想、二分法的思想、恒成立的思想以及问题转化的思想.值得同学们体会反思.

练习册系列答案
相关题目