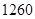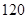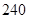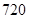题目内容
已知 的展开式中,奇数项的二项式系数之和是64,则
的展开式中,奇数项的二项式系数之和是64,则 的展开式中,
的展开式中, 的系数是( )
的系数是( )
| A.280 | B.-280 | C.-672 | D.672 |
A
解析试题分析:因为 的展开式中,奇数项的二项式系数之和是64,在二项展开式中,奇数项的二项式系数之和与偶数项系数之和相等。所以
的展开式中,奇数项的二项式系数之和是64,在二项展开式中,奇数项的二项式系数之和与偶数项系数之和相等。所以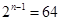 ,n=7,
,n=7,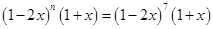 ,其展开式中
,其展开式中 的项是
的项是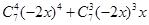 ,系数为280.
,系数为280.
考点:本题主要考查二项式系数的性质,二项式定理。
点评:中档题,在二项展开式中,奇数项的二项式系数之和与偶数项系数之和相等。对计算能力要求较高。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
从5位同学中选派4位同学在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有2人参加,星期六、星期日各有1人参加,则不同的选派方法共有( )
| A.40种 | B.60种 | C.100种 | D.120种 |
从4名男生 和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,
则不同的选法共有 ( )
| A.140种 | B.120种 | C.35种 | D.34种 |
用数字1,2,3,4,5可以组成没有重复数字的五位偶数共有( )
| A.48个 | B.36个 | C.24个 | D.18个 |
从l、2、3、4、5这五个数字中任取3个组成无重复数字的三位数,当三个数字中有2和3时,2需排在3的前面(不一定相邻),这样的三位数有 ( )
| A.51个 | B.54个 | C.12个 | D.45个 |
如图所示是某个区域的街道示意图(每个小矩形的边表示街道),则从A到B的最短线路有( )条
| A.24 | B.60 | C.84 | D.120 |
我们把各位数字之和为6的四位数称为“六合数”(如2013是“六合数”),则“六合数”中首位为2的“六合数”共有
| A.18个 | B.15个 | C.12个 | D.9个 |
已知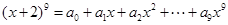 ,则
,则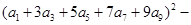
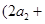
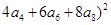 的值为( )
的值为( )
A.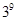 | B.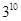 | C.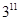 | D.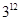 |
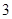 张不同的电影票全部分给
张不同的电影票全部分给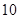 个人,每人至多一张,则有不同分法的种数是( )
个人,每人至多一张,则有不同分法的种数是( )