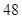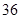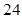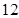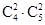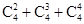题目内容
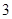张不同的电影票全部分给
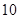个人,每人至多一张,则有不同分法的种数是( )
A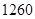． | B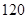． | C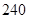． | D． |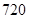
D
解析试题分析：本题是一个分步计数问题，3张不同的电影票全部分给10个人，每人至多一张，第一张有10种结果，第二种有9种结果，第三种有8种结果，根据分步计数原理得到结果。解：由题意知本题是一个分步计数问题，∵3张不同的电影票全部分给10个人，每人至多一张，∴第一张有10种结果，第二种有9种结果，第三种有8种结果，根据分步计数原理有10×9×8=720种结果，故选D．
考点：分步计数问题
点评：本题考查分步计数问题，是一个典型的分步计数问题，题目包含三个环节，看出三个环节的结果数，再根据分步乘法原理得到结果．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
相关题目
，则质点P移动六次后位于点（4，2）的概率是 ( )
在二项式（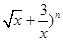
的展开式中，各项系数之和为M，各项二项式系数之和为N，且M+N=72，则展开式中常数项的值为
| A．18 | B．12 | C．9 | D．6 |
已知
的展开式中，奇数项的二项式系数之和是64，则
的展开式中,
的系数是（ ）
| A．280 | B．-280 | C．-672 | D．672 |
有一排7只发光二极管，每只二极管点亮时可发出红光或绿光，若每次恰有3只二极管点亮，且相邻的两只不能同时点亮，根据三只点亮的不同位置，或不同颜色来表示不同的信息，则这排二极管能表示的信息种数共有（ ）种
| A．10 | B．48 | C．60 | D．80 |
若
，则
的值为
A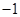． | B．1 | C．2 | D． |
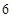人的入园顺序排法种数为（ ）
