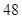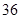题目内容
我们把各位数字之和为6的四位数称为“六合数”(如2013是“六合数”),则“六合数”中首位为2的“六合数”共有
| A.18个 | B.15个 | C.12个 | D.9个 |
B
解析试题分析:四位数之和为6的共有4种情况:(0、0、2、4),(0、1、2、3),(1、1、2、2),(0、2、2、2)。数字为0、0、2、4且首位为2的六合数有:2004,2040,2400,共3个;同理:数字为0、1、2、3且首位为2的六合数有六个;数字为1、1、2、2且首位为2的六合数有3个;数字为0、2、2、2且首位为2的六合数有3个。所以共有15个。
考点:排列、组合。
点评:本题排列、组合的混合问题,我们采取先分组,在排列的方法。此类题为易错题,我们一定要仔细分析。属于中档题。

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
A,B,C,D,E五人并排站成一排,如果A,B必须相邻且B在A的左边,那么不同的排法共有( )
| A.60种 | B.48种 | C.36种 | D.24种 |
已知 的展开式中,奇数项的二项式系数之和是64,则
的展开式中,奇数项的二项式系数之和是64,则 的展开式中,
的展开式中, 的系数是( )
的系数是( )
| A.280 | B.-280 | C.-672 | D.672 |
若 ,则
,则 的值为
的值为
A.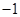 | B.1 | C.2 | D. |
来自高一、高二、高三的铅球裁判员各两名,执行一号、二号和三号场地的铅球裁判工作,每个场地由两名来自不同年级的裁判组成,则不同的安排方案共有( )种.
| A.96 | B.48 | C.36 | D.24 |
若二项式(x+2)n的展开式的第四项是  ,而第三项的二项式系数是15,则x的值为( )
,而第三项的二项式系数是15,则x的值为( )
A.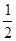 | B. | C. | D. |
已知 (n∈N,n≥1)的展开式中含有常数,则n的最小值是( )
(n∈N,n≥1)的展开式中含有常数,则n的最小值是( )
| A.4 | B.5 | C.9 | D.10 |
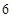 人的入园顺序排法种数为( )
人的入园顺序排法种数为( )