题目内容
13.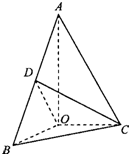 如图,在△AOB中,∠AOB=$\frac{π}{2}$,∠BAO=$\frac{π}{6}$,AB=4,D为线段BA的中点.△AOC由△AOB绕直线AO旋转而成,记∠BOC=θ,θ∈(0,$\frac{π}{2}$].
如图,在△AOB中,∠AOB=$\frac{π}{2}$,∠BAO=$\frac{π}{6}$,AB=4,D为线段BA的中点.△AOC由△AOB绕直线AO旋转而成,记∠BOC=θ,θ∈(0,$\frac{π}{2}$].(1)证明:当θ=$\frac{π}{2}$时,平面COD⊥平面AOB;
(2)当三棱锥D-BOC的体积为1时,求三棱锥A-BOC的全面积.
分析 (1)运用直线平面的垂直,平面的垂直问题之间的转化证明.
(2)运用直角三角形Rt△AOB中,得出DE⊥平面BOC,利用体积公式得出:△BOC是等边三角形,分别求出等腰三角形ABC的面积为$\sqrt{15}$
△AOB与△AOC的面积都是$2\sqrt{3}$,△BOC的面积为$\sqrt{3}$,即可得出三棱锥A-BOC的全面积.
解答 (1)证:当$θ=\frac{π}{2}$时,$∠BOC=\frac{π}{2}$,
即OC⊥OB,
又OC⊥OA,OA∩OB=O
∴OC⊥平面AOB,
∵OC?平面COD
∴平面COD⊥平面AOB.
(2)解:在Rt△AOB中,$AB=4,∠BAO=\frac{π}{6},∠AOB=\frac{π}{2}$
∴$OB=2,OA=2\sqrt{3}$,
取OB的中点E,连接DE,则DE∥AO,
∴$DE=\sqrt{3}$,
又AO⊥平面BOC,
∴DE⊥平面BOC,
∴${V_{D-BOC}}=\frac{1}{3}{S_{△BOC}}•DE=\frac{1}{3}×\frac{1}{2}×2×2sinθ×\sqrt{3}=1$
∴$sinθ=\frac{{\sqrt{3}}}{2}$,$θ=\frac{π}{3}$,
∴△BOC是等边三角形,
∴BC=2
∴等腰三角形ABC的面积为$\sqrt{15}$
△AOB与△AOC的面积都是$2\sqrt{3}$
△BOC的面积为$\sqrt{3}$
∴多面体A-BOC的全面积是$5\sqrt{3}+\sqrt{15}$.
点评 本题考查了空间几何体的性质,面积,公式求解,面面垂直的问题,综合性较强,属于中档题.

练习册系列答案
相关题目
3.在平面直角坐标系xOy中,角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边经过点P(1,1),则函数y=sin(2x+α)在[O,π]上的单调递减区间为( )
| A. | [0,$\frac{π}{8}$]与[$\frac{5π}{8},π$] | B. | [$\frac{3π}{8}$,$\frac{5π}{8}$] | C. | [0,$\frac{π}{8}$]与[$\frac{3π}{8}$,$\frac{5π}{8}$] | D. | [$\frac{π}{8},\frac{5π}{8}$] |