题目内容
(本小题满分10分)
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC, ,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.

已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
 ,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.

(Ⅰ)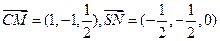 ,因为
,因为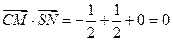 ,
,
所以CM⊥SN
(Ⅱ)SN与平面CMN所成角为45°
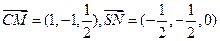 ,因为
,因为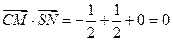 ,
,所以CM⊥SN
(Ⅱ)SN与平面CMN所成角为45°
证明:则P(0,0,1),C(0,1,0),B(2,0,0),M(1,0,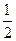 ),N(
),N(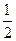 ,0,0),S(1,
,0,0),S(1,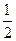 ,0).
,0).
(Ⅰ)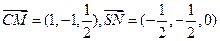 ,因为
,因为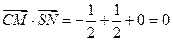 ,
,
所以CM⊥SN
(Ⅱ)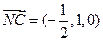 ,设a=(x,y,z)为平面CMN的一个法向量,
,设a=(x,y,z)为平面CMN的一个法向量,
则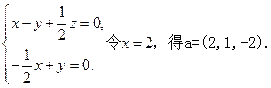 因为
因为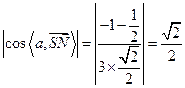 ,
,
所以SN与平面CMN所成角为45°
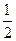 ),N(
),N(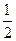 ,0,0),S(1,
,0,0),S(1,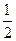 ,0).
,0).(Ⅰ)
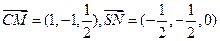 ,因为
,因为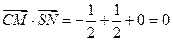 ,
,所以CM⊥SN
(Ⅱ)
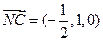 ,设a=(x,y,z)为平面CMN的一个法向量,
,设a=(x,y,z)为平面CMN的一个法向量,则
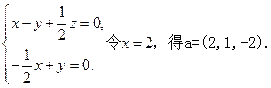 因为
因为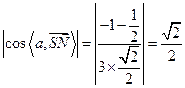 ,
,所以SN与平面CMN所成角为45°

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
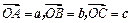 ,可构成空间向量的一个基底,若
,可构成空间向量的一个基底,若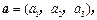
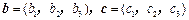 ,在向量已有的运算法则的基础上,新定义一种运算
,在向量已有的运算法则的基础上,新定义一种运算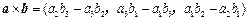 ,显然
,显然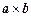 的结果仍为一向量,记作
的结果仍为一向量,记作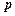 .
.
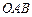 的法向量;
的法向量;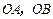 为边的平行四边形
为边的平行四边形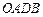 的面积等于
的面积等于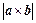 ;
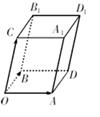
;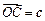 平移,得到一个平行六面体
平移,得到一个平行六面体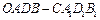 ,试判断平行六面体的体积
,试判断平行六面体的体积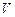 与
与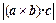 的大小.
的大小.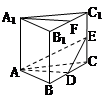
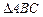 是边长为2的等边三角形,
是边长为2的等边三角形,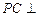 平面
平面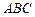 ,
,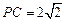 ,
,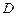 是
是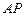 上一动点.
上一动点.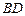 与平面
与平面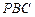 所成的角的正弦值;
所成的角的正弦值;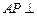 平面
平面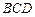 ?请说明理
?请说明理 由.
由.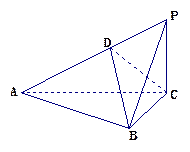
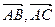 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S; 分别与向量
分别与向量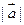 =
=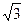 ,求向量
,求向量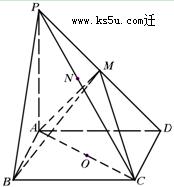
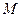 是PC的中点,设
是PC的中点,设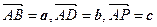 .
.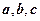 表示出向量
表示出向量 ;
;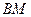 的长.
的长.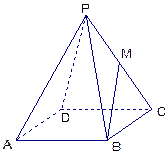
 中,若
中,若 则
则 ( )
( )

