题目内容
圆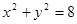 内有一点
内有一点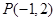 ,
,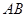 为过点
为过点 且倾斜角为
且倾斜角为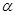 的弦,
的弦,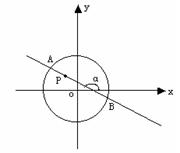
(1)当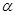 =1350时,求
=1350时,求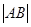 ;
;
(2)当弦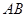 被点
被点 平分时,求出直线
平分时,求出直线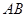 的方程;
的方程;
(3)设过 点的弦的中点为
点的弦的中点为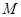 ,求点
,求点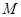 的坐标所满足的关系式.
的坐标所满足的关系式.
(1)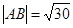 (2)
(2) 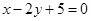 (3)
(3)
解析试题分析:(1)要求弦长,可利用弦长公式,即将弦所在的直线方程,与圆的方程联立,之后所得的二次方程中,利用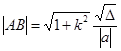 求之.还可以利用圆中
求之.还可以利用圆中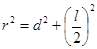 求之,其中
求之,其中 是圆心到弦所在直线的距离,
是圆心到弦所在直线的距离,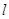 指弦长.但是不论采取哪种方法,都先得求出弦所在的直线方程.根据题意,点斜式可求出.
指弦长.但是不论采取哪种方法,都先得求出弦所在的直线方程.根据题意,点斜式可求出.
(2)当弦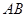 被
被 平分时,弦
平分时,弦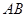 所在直线被直线
所在直线被直线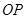 垂直且平分.所以,可先求出直线
垂直且平分.所以,可先求出直线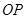 斜率, 根据垂直可知直线
斜率, 根据垂直可知直线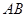 斜率,又因为直线
斜率,又因为直线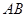 过点
过点 ,根据点斜式可求出直线
,根据点斜式可求出直线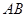 .
.
(3)因为过点 的弦可分为三种情况,①无斜率,此时
的弦可分为三种情况,①无斜率,此时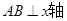 ,
,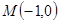 ;②斜率为0,此时
;②斜率为0,此时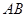 平行x轴,
平行x轴,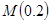 ;③直线
;③直线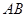 有斜率,且不为0,此时
有斜率,且不为0,此时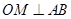 ,根据斜率相乘等于-1可找到
,根据斜率相乘等于-1可找到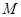 点轨迹,将①②代入③中验证即可.
点轨迹,将①②代入③中验证即可.
试题解析:(1)当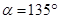 时,直线
时,直线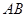 的斜率为-1,根据点斜式有,直线
的斜率为-1,根据点斜式有,直线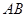 的方程
的方程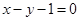 ,
,
所以圆心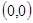 到直线
到直线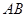 的距离为
的距离为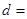
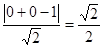 ,又因为
,又因为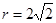 ,
,
所以根据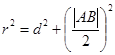 ,解得
,解得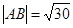

(2)当弦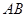 被
被 平分时,
平分时,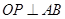 ,
,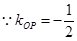 ,
,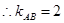
又因为直线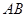 过点
过点 ,所以根据点斜式有直线
,所以根据点斜式有直线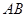 的方程为
的方程为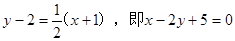 .
.
(3)设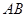 的中点为
的中点为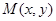 ,则
,则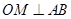 ,即
,即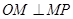
当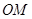 的斜率和
的斜率和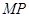 的斜率都存在时:有
的斜率都存在时:有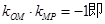
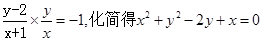
当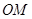 斜率不存在时点
斜率不存在时点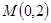 满足上式,
满足上式,
当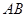 斜率不存在时点
斜率不存在时点 亦满足上式,
亦满足上式,
所以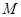 点的轨迹为
点的轨迹为 。
。
考点:求圆中的弦长;点斜式求直线;讨论直线斜率情况求点的轨迹.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,点
,点 依次满足
依次满足 。
。 的轨迹;
的轨迹;  作直线
作直线 交以
交以 为焦点的椭圆于
为焦点的椭圆于 两点,线段
两点,线段 的中点到
的中点到 轴的距离为
轴的距离为 ,且直线
,且直线 的坐标为
的坐标为 ,是否存在椭圆上的点
,是否存在椭圆上的点 及以
及以 都相切,如存在,求出
都相切,如存在,求出
 ,求直线l的方程;
,求直线l的方程;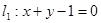 ,
,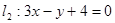 , 且它的对角线的交点是M(3,3),求这个平行四边形其它两边所在直线的方程.
, 且它的对角线的交点是M(3,3),求这个平行四边形其它两边所在直线的方程. ,则方程
,则方程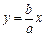 表示不同的直线有__________条.
表示不同的直线有__________条.