题目内容
13．圆（x-1）2+（y+2）2=5上的点到直线y=2x+6的最短距离为$\sqrt{5}$．分析 利用点到直线的距离公式，算出圆心C到直线y=2x+6的距离，用这个距离减去圆的半径就是所求点到直线距离的最小值，由此可得本题的答案．
解答 解：∵圆（x-1）2+（y+2）2=5的圆心为C（1，-2），半径r=$\sqrt{5}$，
∴圆心C到直线2x-y+6=0的距离为d=$\frac{|2+2+6|}{\sqrt{4+1}}$=2$\sqrt{5}$．
因此，圆（x-1）2+（y+2）2=5上的点到直线y=2x+6的最短距离为d-r=$\sqrt{5}$．
故答案为：$\sqrt{5}$．
点评 本题给出定圆与直线，求圆上的点到直线距离的最小值．着重考查了圆的标准方程、点到直线的距离公式和直线与圆的位置关系等知识，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
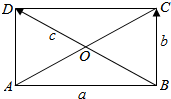如图所示，已知在矩形ABCD中，|$\overrightarrow{AD}$|=4$\sqrt{3}$，|$\overrightarrow{AB}$|=8，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，$\overrightarrow{BD}$=$\overrightarrow{c}$，求|$\overrightarrow{a}-\overrightarrow{b}-\overrightarrow{c}$|
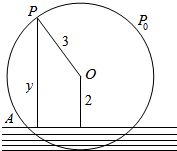如图为一半径是3米的水轮，水轮圆心O距离水面2米，开始旋转时水轮上的点P在P0位置，P0距离水面3米，已知水轮每分钟旋转4圈，求点P到水面的距离y（米）与时间x（秒）的函数关系式．