题目内容
甲厂以x 千克/小时的速度运输生产某种产品(生产条件要求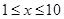 ),每小时可获得利润是
),每小时可获得利润是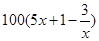 元.
元.
(1)要使生产该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求最大利润.
(1) 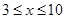 (2)
(2) 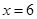 时,
时,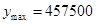 元
元
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
甲厂以x 千克/小时的速度运输生产某种产品(生产条件要求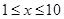 ),每小时可获得利润是
),每小时可获得利润是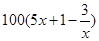 元.
元.
(1)要使生产该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求最大利润.
(1) 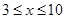 (2)
(2) 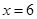 时,
时,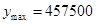 元
元
解析

 阅读快车系列答案
阅读快车系列答案