题目内容
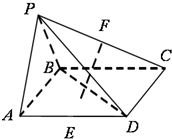
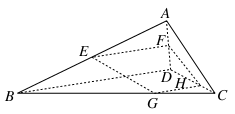
如图，已知在空间四边形ABCD中，E，F分别是AB，AD的中点，G，H分别是BC，CD上的点，且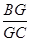
＝
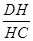＝2.求证：直线EG，FH，AC相交于一点．
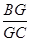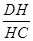＝＝2.求证：直线EG，FH，AC相交于一点．见解析
解：∵E，F分别是AB，AD的中点，
∴EF∥BD，EF＝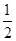
BD.
又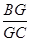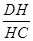＝＝2，∴GH∥BD，GH＝
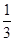BD，
∴EF∥GH，EF＝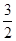
GH，
∴四边形EFHG是梯形，设两腰EG，FH相交于一点T.
∵EG?平面ABC，FH?平面ACD，∴T∈平面ABC，且T∈平面ACD，又平面ABC∩平面ACD＝AC，
∴T∈AC，即直线EG，FH，AC相交于一点T.
∴EF∥BD，EF＝
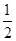BD.又
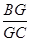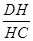＝＝2，∴GH∥BD，GH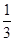＝BD，∴EF∥GH，EF＝
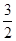GH，∴四边形EFHG是梯形，设两腰EG，FH相交于一点T.
∵EG?平面ABC，FH?平面ACD，∴T∈平面ABC，且T∈平面ACD，又平面ABC∩平面ACD＝AC，
∴T∈AC，即直线EG，FH，AC相交于一点T.
练习册系列答案
相关题目
