题目内容
6.若x>1,则求函数y=$\frac{2x{\;}^{2}-x+1}{x-1}$的最小值.分析 将函数变形,再结合不等式的性质即可.
解答 解:y=$\frac{2x{\;}^{2}-x+1}{x-1}$
=$\frac{2{x}^{2}-4x+2+2+3x-3}{x-1}$
=$\frac{2(x-1)^{2}+2+3(x-1)}{x-1}$
=2(x-1)+$\frac{2}{x-1}$+3
≥2$\sqrt{2(x-1)×\frac{2}{x-1}}$+3 (∵x>1,即x-1>0)
=2×2+3=7,
当且仅当$2(x-1)=\frac{2}{x-1}$,即x=2或x=0(舍)时成立,
即函数y的最小值为7.
点评 本题考查求函数的最值及不等式的性质,要注意函数表达式的灵活变形,属于基础题.

练习册系列答案
相关题目
11.i是虚数单位,复数$\frac{5-2i}{2+5i}$=( )
| A. | -i | B. | i | C. | -$\frac{21}{29}$-$\frac{20}{29}$i | D. | -$\frac{4}{21}$+$\frac{10}{21}$i |
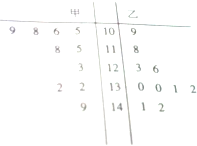 如图记录了甲、乙两名同学其中10次数学成绩.
如图记录了甲、乙两名同学其中10次数学成绩.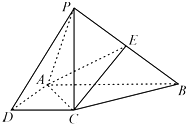 如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,
如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,