题目内容
设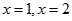 是
是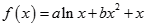 函数的两个极值点.
函数的两个极值点.
(1)试确定常数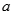 和
和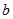 的值;
的值;
(2)试判断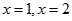 是函数
是函数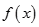 的极大值点还是极小值点,并求出相应极值.
的极大值点还是极小值点,并求出相应极值.
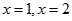 是
是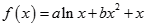 函数的两个极值点.
函数的两个极值点.(1)试确定常数
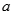 和
和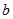 的值;
的值;(2)试判断
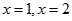 是函数
是函数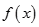 的极大值点还是极小值点,并求出相应极值.
的极大值点还是极小值点,并求出相应极值.(1)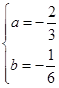 ;(2)在
;(2)在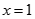 处,函数
处,函数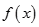 取极小值
取极小值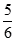 ;在
;在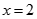 处,函数
处,函数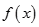 取得极大值
取得极大值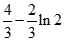 .
.
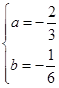 ;(2)在
;(2)在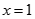 处,函数
处,函数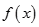 取极小值
取极小值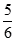 ;在
;在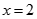 处,函数
处,函数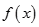 取得极大值
取得极大值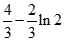 .
.试题分析:(1)先求出导函数
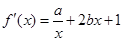 ,接着由题中条件得到
,接着由题中条件得到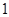 与
与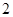 是方程
是方程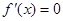 的两个根,进而得出
的两个根,进而得出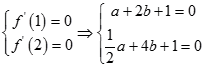 ,从中求解方程组即可得到
,从中求解方程组即可得到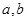 的值;(2)根据(1)中确定的函数的解析式,求出导函数
的值;(2)根据(1)中确定的函数的解析式,求出导函数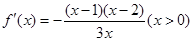 ,列表得到:
,列表得到: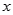 变化时,
变化时,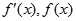 的变化情况,进而确定函数的极大值与极小值.
的变化情况,进而确定函数的极大值与极小值.试题解析:(1)
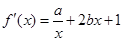
由已知得:
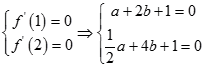
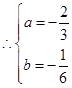
(2)由(1)得
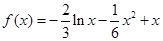 ,
,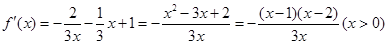
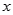 变化时.
变化时.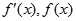 的变化情况如表:
的变化情况如表: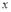 | 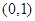 | 1 | 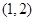 | 2 | 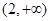 |
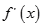 | — | 0 | + | 0 | — |
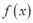 |  | 极小值 |  | 极大值 | 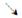 |
故在
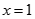 处,函数
处,函数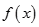 取极小值
取极小值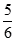 ;在
;在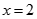 处,函数
处,函数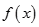 取得极大值
取得极大值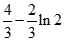 .
.
练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
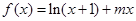 ,当
,当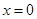 时,函数
时,函数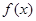 取得极大值.
取得极大值.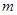 的值;
的值;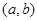 内导数都存在,且
内导数都存在,且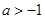 ,则存在
,则存在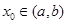 ,使得
,使得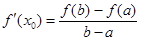 .试用这个结论证明:若
.试用这个结论证明:若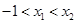 ,函数
,函数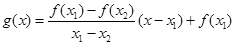 ,则对任意
,则对任意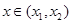 ,都有
,都有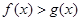 ;
;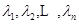 ,满足
,满足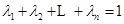 ,求证:当
,求证:当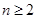 ,
,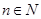 时,对任意大于
时,对任意大于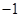 ,且互不相等的实数
,且互不相等的实数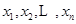 ,都有
,都有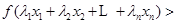
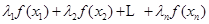 .
. 在
在 时有极值0,则
时有极值0,则 [o___.
[o___.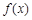 ,若对任意
,若对任意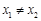 ,都
,都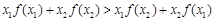 ,则称f(x)为“H函数”,给出下列函数:①
,则称f(x)为“H函数”,给出下列函数:①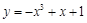 ;②
;② ;③
;③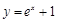 ;④
;④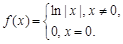 其中是“H函数”的个数为( ).
其中是“H函数”的个数为( ).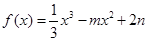 (
(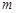 ,
,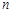 为常数),当
为常数),当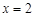 时,函数
时,函数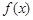 有极值,若函数
有极值,若函数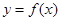 有且只有三个零点,则实数
有且只有三个零点,则实数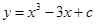 的图像与
的图像与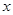 轴恰有两个公共点,则
轴恰有两个公共点,则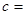 ( )
( ) ,1)
,1)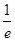
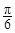 是函数
是函数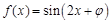 的一个零点,则函数
的一个零点,则函数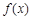 在区间
在区间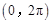 内所有极值点之和为
内所有极值点之和为