题目内容
首项为 的等差数列,从第10项起开始为正数,则公差
的等差数列,从第10项起开始为正数,则公差 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
C
解析试题分析:先设数列为{an}公差为d,则a1=-24,根据等差数列的通项公式,分别表示出a10和a9,进而根据a10>0,a9≤0求得d的范围.解:设数列为{an}公差为d,则a1=-24; a10=a1+9d>0;即9d>24,所以d>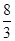
而a9=a1+8d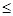 0;,即d≤3,所以
0;,即d≤3,所以 ,故选C
,故选C
考点:等差数列
点评:本题主要考查了等差数列的性质.属基础题.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
已知等差数列 中,
中, ,则
,则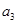 =( )
=( )
| A.10 | B.20 | C.30 | D.40 |
已知数列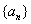 是等差数列
是等差数列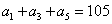 ,
,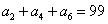 ,
,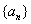 的前
的前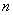 项和为
项和为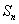 ,则使得
,则使得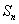 达到最大的
达到最大的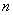 是( )
是( )
| A.18 | B.19 | C.20 | D.21 |
已知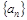 为等差数列,其前
为等差数列,其前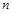 项和为
项和为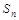 ,若
,若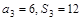 ,则公差
,则公差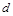 等于( )
等于( )
A.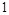 | B. | C.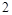 | D.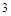 |
在等差数列 中,若
中,若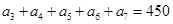 ,则
,则 的值等于( )
的值等于( )
| A.45 | B.75 | C.180 | D.300 |
等差数列 ,
,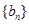 的前
的前 项和分别为
项和分别为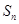 ,
, ,若
,若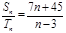 ,则使
,则使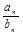 为整数的正整数n的取值个数是( )
为整数的正整数n的取值个数是( )
| A. 3 | B. 4 | C. 5 | D. 6 |
设等差数列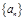 的前n项和为
的前n项和为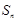 ,若
,若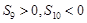 ,则
,则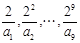 中最大的是
中最大的是
A.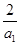 | B.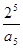 | C.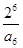 | D. |
各项都为正数的等比数列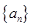 的公比
的公比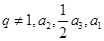 成等差数列,则
成等差数列,则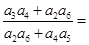 ( )
( )
A.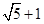 | B.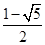 | C.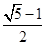 | D. |
等差数列{an}共有2n+1项,其中奇数项之和为4,偶数项之和为3,则n的值是
| A.3 | B.5 | C.7 | D.9 |