题目内容
等差数列{an}共有2n+1项，其中奇数项之和为4，偶数项之和为3，则n的值是
| A．3 | B．5 | C．7 | D．9 |
A
解析试题分析：利用等差数列的求和公式和性质得出
，来解得。解：设数列公差为d，首项为a1，奇数项共n+1项，其和为S奇=（n+1）an+1=4，偶数项共n项，其和为S偶=nan+1=3，由，可知n的值为3，选A.
考点：等差数列的求和公式
点评:本题考查等差数列的求和公式和性质，熟练记忆并灵活运用求和公式是解题的关键，属基础题
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
首项为
的等差数列，从第10项起开始为正数，则公差
的取值范围是 ( )
A． | B． | C． | D． |
已知等差数列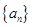
的前
项和为
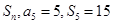,则数列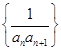
的前100项和为（ ）
A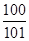． | B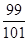． | C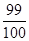． | D． |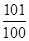
等差数列
， an=2n+1,则a3= （ ）
| A．5 | B．7 | C．6 | D．8 |
等差数列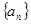
前
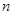项和为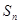
，
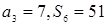，则公差d的值为
| A．2 | B．3 | C．-3 | D．4 |
设
是等差数列，
是其前
项的和，且
，
，则下列结论错误的是
A． | B． |
C． | D． 和 均为的最大值 |
已知数列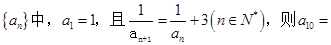
| A．28 | B．33 | C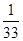． | D． |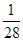
若等差数列{an}的前5项之和S5＝25，且a2＝3，则a7＝( )
| A．12 | B．13 | C．14 | D．15 |
等差数列{an}中，a1，a2，a3分别是下表第一、二、三行中的某一个数，且a1，a2，a3中的任何两个数不在下表的同一列。
| | 第一列 | 第二列 | 第三列 |
| 第一行 | 2 | 3 | 5 |
| 第二行 | 8 | 6 | 14 |
| 第三行 | 11 | 9 | 13 |
则a4的值为
A．18 B．15 C．12 D．20