题目内容
记函数f(x)的导数为f(1)(x),f(1)(x)的导数为f(2)(x),…f(n-1)(x)的导数为f(n)(x)(n∈N*).若f(x)可进行n次求导,则f(x)均可近似表示为:f(x)≈f(0)+
x+
x2+
x3+…+
xn,其中n!=n(n-1)(n-2)(n-3)…3×2×1,若取n=3,根据这个结论,则可近似估计自然对数的底数e≈
(用分数表示).
| f(1)(0) |
| 1! |
| f(2)(0) |
| 2! |
| f(3)(0) |
| 3! |
| f(n)(0) |
| n! |
| 8 |
| 3 |
| 8 |
| 3 |
分析:利用(ex)(n)=ex及其所给的展开式即可得出.
解答:解:令f(x)=ex,则f′(x)=f″(x)=f(3)(x)=ex,且f′(0)=f″(0)=f(3)(0)=1.
∴e=f(1)≈e0+
×1+
×12+
×13
即e≈1+1+
+
=
.
故答案为
.
∴e=f(1)≈e0+
| 1 |
| 1! |
| 1 |
| 2! |
| 1 |
| 3! |
即e≈1+1+
| 1 |
| 2×1 |
| 1 |
| 3×2×1 |
| 8 |
| 3 |
故答案为
| 8 |
| 3 |
点评:熟练掌握(ex)(n)=ex及正确理解所给的展开式是解题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
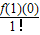 x+
x+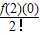 x2+
x2+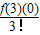 x3+…+
x3+…+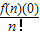 xn,其中n!=n(n-1)(n-2)(n-3)…3×2×1,若取n=3,根据这个结论,则可近似估计自然对数的底数e≈ (用分数表示).
xn,其中n!=n(n-1)(n-2)(n-3)…3×2×1,若取n=3,根据这个结论,则可近似估计自然对数的底数e≈ (用分数表示).