题目内容
记函数f(x)的导数为f(1)(x),f(1)(x)的导数为f(2)(x),…,f(n-1)(x)的导数为f(n)(x)(n∈N*).若f(x)可进行n次求导,则f(x)均可近似表示为:
若取n=4,根据这个结论,则可近似估计自然对数的底数e≈
(用分数表示)(注:n!=n×(n-1)×…×2×1)
|
若取n=4,根据这个结论,则可近似估计自然对数的底数e≈
| 65 |
| 24 |
| 65 |
| 24 |
分析:令f(x)=ex,由已知,将f(x)近似表示为f(0)+x+
+
+
,令x=1,则能得出关于e的表达式,整理计算即可.
| x |
| 2 |
| x |
| 6 |
| x |
| 24 |
解答:解:构造函数f(x)=ex,根据导数运算,可知f(n)(x)=ex,f(n)(0)=1
所以若取n=4,ex≈f(0)+x+
+
+
,
令x=1,则e≈1+1+
+
+
=
故答案为:
所以若取n=4,ex≈f(0)+x+
| x |
| 2 |
| x |
| 6 |
| x |
| 24 |
令x=1,则e≈1+1+
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 24 |
| 65 |
| 24 |
故答案为:
| 65 |
| 24 |
点评:本题考查函数求导运算,阅读、转化、构造、计算能力.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
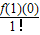 x+
x+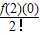 x2+
x2+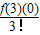 x3+…+
x3+…+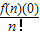 xn,其中n!=n(n-1)(n-2)(n-3)…3×2×1,若取n=3,根据这个结论,则可近似估计自然对数的底数e≈ (用分数表示).
xn,其中n!=n(n-1)(n-2)(n-3)…3×2×1,若取n=3,根据这个结论,则可近似估计自然对数的底数e≈ (用分数表示).