题目内容
设函数f(x)=ax+bx-cx,其中c>a>0,c>b>0.
(1)记集合M={(a,b,c)|a、b、c不能构成一个三角形的三条边长,且a=b},则(a,b,c)∈M所对应的f(x)的零点的取值集合为________.
(2)若a、b、c是△ABC的三条边长,则下列结论正确的是________.(填序号)
①?x∈(-∞,1),f(x)>0;
②?x∈R,使ax、bx、cx不能构成一个三角形的三条边长;
③若△ABC为钝角三角形,则?x∈(1,2),使f(x)=0.
(1)记集合M={(a,b,c)|a、b、c不能构成一个三角形的三条边长,且a=b},则(a,b,c)∈M所对应的f(x)的零点的取值集合为________.
(2)若a、b、c是△ABC的三条边长,则下列结论正确的是________.(填序号)
①?x∈(-∞,1),f(x)>0;
②?x∈R,使ax、bx、cx不能构成一个三角形的三条边长;
③若△ABC为钝角三角形,则?x∈(1,2),使f(x)=0.
(1){x|0<x≤1} (2)①②③
(1)因为c>a>0,c>b>0,a=b且a、b、c不能构成一个三角形的三条边长,
所以0<2a≤c,所以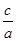 ≥2.
≥2.
令f(x)=0,得2ax=cx,即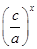 =2,即x=
=2,即x=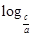 2,
2,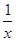 =log2
=log2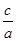 ≥1,所以0<x≤1.
≥1,所以0<x≤1.
(2)由a、b、c是△ABC的三条边长,知a+b>c,
因为c>a>0,c>b>0,所以0<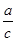 <1,0<
<1,0<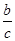 <1,
<1,
当x∈(-∞,1)时,f(x)=ax+bx-cx=cx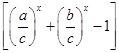 >cx
>cx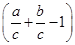 =cx·
=cx·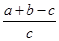 >0,①正确;
>0,①正确;
令a=2,b=3,c=4,则a、b、c可以构成三角形,而a2=4,b2=9,c2=16不能构成三角形,②正确;
由c>a,c>b,且△ABC为钝角三角形,则a2+b2-c2<0.因为f(1)=a+b-c>0,f(2)=a2+b2-c2<0,所以f(x)在(1,2)上存在零点,③正确
所以0<2a≤c,所以
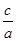 ≥2.
≥2.令f(x)=0,得2ax=cx,即
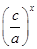 =2,即x=
=2,即x=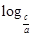 2,
2,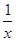 =log2
=log2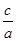 ≥1,所以0<x≤1.
≥1,所以0<x≤1.(2)由a、b、c是△ABC的三条边长,知a+b>c,
因为c>a>0,c>b>0,所以0<
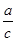 <1,0<
<1,0<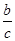 <1,
<1,当x∈(-∞,1)时,f(x)=ax+bx-cx=cx
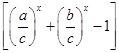 >cx
>cx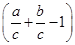 =cx·
=cx·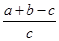 >0,①正确;
>0,①正确;令a=2,b=3,c=4,则a、b、c可以构成三角形,而a2=4,b2=9,c2=16不能构成三角形,②正确;
由c>a,c>b,且△ABC为钝角三角形,则a2+b2-c2<0.因为f(1)=a+b-c>0,f(2)=a2+b2-c2<0,所以f(x)在(1,2)上存在零点,③正确

练习册系列答案
相关题目
 则满足不等式f(f(x))>1的x的取值范围是________.
则满足不等式f(f(x))>1的x的取值范围是________.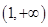 上恒取正值.
上恒取正值.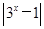 的图象,并利用图象回答:k为何值时,方程
的图象,并利用图象回答:k为何值时,方程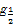 x,实数a,b,c满足a<b<c,且满足f(a)f(b)f(c)<0,若实数x0是函数y=f(x)的一个零点,则下列结论一定成立的是( )
x,实数a,b,c满足a<b<c,且满足f(a)f(b)f(c)<0,若实数x0是函数y=f(x)的一个零点,则下列结论一定成立的是( )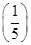 x-log3x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)的值 ( ).
x-log3x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)的值 ( ).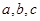 为正实数,
为正实数,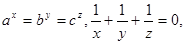 则
则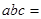 .
.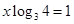 ,则
,则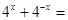 ()
()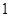

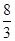
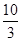
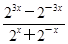 的值.
的值.