题目内容
已知在直角坐标系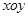 中,曲线
中,曲线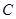 的参数方程为
的参数方程为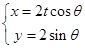 (
(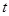 为非零常数,
为非零常数,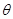 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系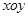 取相同的长度单位,且以原点
取相同的长度单位,且以原点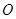 为极点,以
为极点,以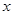 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线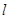 的方程为
的方程为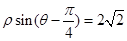 .
.
(Ⅰ)求曲线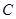 的普通方程并说明曲线的形状;
的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数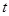 ,使得直线
,使得直线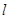 与曲线
与曲线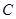 有两个不同的公共点
有两个不同的公共点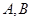 ,且
,且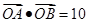 (其中
(其中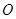 为坐标原点)?若存在,请求出;否则,请说明理由.
为坐标原点)?若存在,请求出;否则,请说明理由.
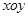 中,曲线
中,曲线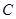 的参数方程为
的参数方程为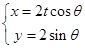 (
(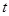 为非零常数,
为非零常数,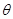 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系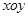 取相同的长度单位,且以原点
取相同的长度单位,且以原点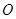 为极点,以
为极点,以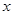 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线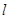 的方程为
的方程为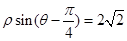 .
.(Ⅰ)求曲线
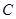 的普通方程并说明曲线的形状;
的普通方程并说明曲线的形状;(Ⅱ)是否存在实数
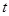 ,使得直线
,使得直线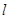 与曲线
与曲线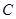 有两个不同的公共点
有两个不同的公共点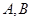 ,且
,且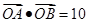 (其中
(其中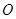 为坐标原点)?若存在,请求出;否则,请说明理由.
为坐标原点)?若存在,请求出;否则,请说明理由.(1)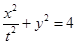 ,当
,当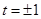 时,曲线C为圆心在原点,半径为2的圆,当
时,曲线C为圆心在原点,半径为2的圆,当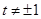 时,曲线C为中心在原点的椭圆;(2)不存在.
时,曲线C为中心在原点的椭圆;(2)不存在.
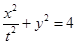 ,当
,当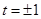 时,曲线C为圆心在原点,半径为2的圆,当
时,曲线C为圆心在原点,半径为2的圆,当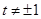 时,曲线C为中心在原点的椭圆;(2)不存在.
时,曲线C为中心在原点的椭圆;(2)不存在.试题分析:(1)先将曲线
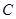 的参数方程转化为普通方程,讨论
的参数方程转化为普通方程,讨论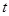 的值来判断方程表示什么图形;(2)联立直线与曲线的方程,因为直线与曲线有2个不同的公共点,所以判别式大于0,所以
的值来判断方程表示什么图形;(2)联立直线与曲线的方程,因为直线与曲线有2个不同的公共点,所以判别式大于0,所以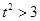 ,利用韦达定理将
,利用韦达定理将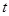 的关系代入
的关系代入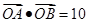 中,解出
中,解出 与
与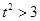 相矛盾,所以不存在
相矛盾,所以不存在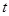 .
.试题解析:(Ⅰ)∵
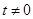 ,∴可将曲线C的方程化为普通方程:
,∴可将曲线C的方程化为普通方程: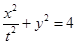 . 2分
. 2分①当
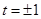 时,曲线C为圆心在原点,半径为2的圆; 4分
时,曲线C为圆心在原点,半径为2的圆; 4分②当
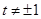 时,曲线C为中心在原点的椭圆. 6分
时,曲线C为中心在原点的椭圆. 6分(Ⅱ)直线
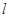 的普通方程为:
的普通方程为: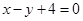 . 8分
. 8分联立直线与曲线的方程,消
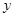 得
得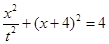 ,化简得
,化简得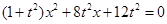 .
.若直线
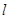 与曲线C有两个不同的公共点,则
与曲线C有两个不同的公共点,则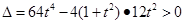 ,解得
,解得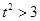 .
.又
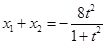 ,
,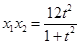 10分
10分故
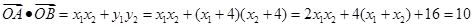 .
.解得
 与
与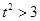 相矛盾. 故不存在满足题意的实数
相矛盾. 故不存在满足题意的实数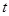 . 12分
. 12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
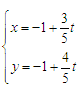 (为参数),曲线C的极坐标方程为
(为参数),曲线C的极坐标方程为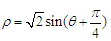 .
.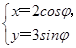 (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=2.正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=2.正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为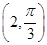 ,
,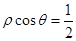 与曲线
与曲线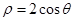 相交于
相交于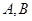 两点,
两点,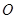 为极点,则
为极点,则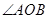 的大小为 .
的大小为 .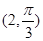 到圆
到圆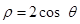 的圆心的距离为( ).
的圆心的距离为( ).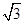 C.
C. 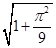 D
D 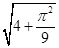
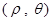 (
(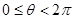 )中,直线
)中,直线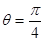 被圆
被圆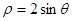 截得的弦长是 .
截得的弦长是 .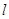 的方程为
的方程为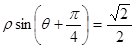 ,则点
,则点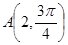 到直线
到直线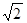
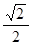
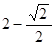
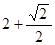
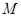 点的极坐标为
点的极坐标为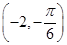 ,则
,则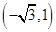
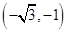
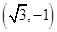
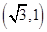
 化成直角坐标为
化成直角坐标为