题目内容
函数f(x)=3x-4x3,x∈[0,1]的最小值是
- A.1
- B.1.5
- C.0
- D.-1
D
分析:由f(x)=3x-4x3,知f′(x)=3-12x2,令f′(x)=3-12x2=0,得x=± .由此能求出函数f(x)=3x-4x3,x∈[0,1]的最小值.
.由此能求出函数f(x)=3x-4x3,x∈[0,1]的最小值.
解答:∵f(x)=3x-4x3,
∴f′(x)=3-12x2,
令f′(x)=3-12x2=0,
得x=± .
.
∵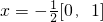 ,
,
∴x=- (舍).
(舍).
∵f(0)=0,f( )=
)=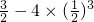 =1,f(1)=3-4=-1.
=1,f(1)=3-4=-1.
∴函数f(x)=3x-4x3,x∈[0,1]的最小值是-1.
故选D.
点评:本题考查函数的最小值的求法,是基础题,解题时要认真审题,仔细解答.如本题解答中没有研究单调性,于课本例题解答步骤不同,但在最值一定是在极值与端点值取到这一规律下,这一解答方式就规避了单调性的讨论,使得运算量降低,解题时可参考技巧降低解题难度
分析:由f(x)=3x-4x3,知f′(x)=3-12x2,令f′(x)=3-12x2=0,得x=±
 .由此能求出函数f(x)=3x-4x3,x∈[0,1]的最小值.
.由此能求出函数f(x)=3x-4x3,x∈[0,1]的最小值.解答:∵f(x)=3x-4x3,
∴f′(x)=3-12x2,
令f′(x)=3-12x2=0,
得x=±
 .
.∵
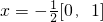 ,
,∴x=-
 (舍).
(舍).∵f(0)=0,f(
 )=
)=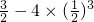 =1,f(1)=3-4=-1.
=1,f(1)=3-4=-1.∴函数f(x)=3x-4x3,x∈[0,1]的最小值是-1.
故选D.
点评:本题考查函数的最小值的求法,是基础题,解题时要认真审题,仔细解答.如本题解答中没有研究单调性,于课本例题解答步骤不同,但在最值一定是在极值与端点值取到这一规律下,这一解答方式就规避了单调性的讨论,使得运算量降低,解题时可参考技巧降低解题难度

练习册系列答案
相关题目
已知函数f(x)=
+1,则
的值为( )
| 3 | x |
| lim |
| △x→0 |
| f(1-△x)-f(1) |
| △x |
A、-
| ||
B、
| ||
C、
| ||
| D、0 |