Question

【题目】设抛物线的顶点为坐标原点,焦点在轴的正半轴上,点是抛物线上的一点，以为圆心,2为半径的圆与轴相切,切点为.

(I)求抛物线的标准方程:

(Ⅱ)设直线在轴上的截距为6,且与抛物线交于,两点,连接并延长交抛物线的准线于点,当直线恰与抛物线相切时,求直线的方程.

Answer 1

【答案】（Ⅰ）.

(Ⅱ) 直线的方程为或.

【解析】试题分析：

（Ⅰ）设抛物线方程为，由以为圆心，2为半径的圆与轴相切，切点为，可得，故所求方程为．（Ⅱ）由题意设出直线的方程为，并设，由导数的几何意义可得抛物线在点处的切线方程为，令，可得．根据三点共线得，整理得

，然后结合根与系数的关系可解得，于是可得直线的方程．

试题解析：

（Ⅰ）设抛物线方程为，

∵以为圆心，2为半径的圆与轴相切，切点为，

∴，

∴该抛物线的标准方程为.

（Ⅱ）由题知直线的斜率存在，设其方程为，

由消取整理得，

显然，．

设，则.

抛物线在点处的切线方程为，

令，得，可得点，

由三点共线得，

∴，即，

整理得,

∴

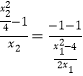解得，即，

∴所求直线的方程为或.