题目内容
设命题p:平面α∩平面β=l,若m⊥l,则m⊥β;命题q:函数y=cos(x-
)的图象关于直线x=
对称.则下列判断正确的是( )
| π |
| 2 |
| π |
| 2 |
| A.p为真 | B.¬q为假 | C.p∨q为假 | D.p∧q为真 |
由命题p:
∵m⊥l,
∴m∥β或m⊥β或m?β,
∴命题p为假命题;
由命题q得:
y=cos(x-
)=cos(
-x)=sinx,
∴y=sinx的图象关于直线x=
对称.
∴命题q为真命题;
∴命题¬q为假命题;
故选B.
∵m⊥l,
∴m∥β或m⊥β或m?β,
∴命题p为假命题;
由命题q得:
y=cos(x-
| π |
| 2 |
| π |
| 2 |
∴y=sinx的图象关于直线x=
| π |
| 2 |
∴命题q为真命题;
∴命题¬q为假命题;
故选B.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 ”是“
”是“ ”的 条件. (请在“充要”、“充分不必要”、“必要不充分”、“既不充分也不必要”中选择一个合适的填空
”的 条件. (请在“充要”、“充分不必要”、“必要不充分”、“既不充分也不必要”中选择一个合适的填空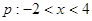 ,条件
,条件 ;若
;若 是
是 的充分而不必要条件,则
的充分而不必要条件,则 的取值范围是 .
的取值范围是 .